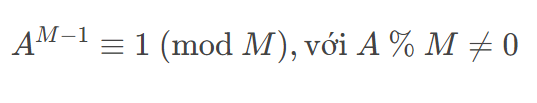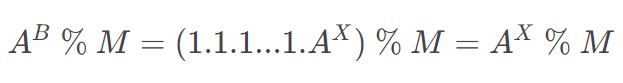IV. Phép nhân Ấn Độ

1. Đặt vấn đề

Xét một bài toán đơn giản như sau: Cho hai số a,b (a,b≤1018)a, btext{ }(a, b le 10^{18})a,b (a,b≤1018). Tính giá trị biểu thức (a×b) % 109(atimes b) text{ }%text{ } 10^9(a×b) % 109.

Bài toán trên có thể dễ dàng giải quyết bằng tính chất phân phối của phép nhân đối với phép đồng dư thức:

(a×b) % 109=[(a % 109)×(b % 109)] % 109(atimes b) text{ }%text{ } 10^9=[(atext{ }%text{ }10^9)times(btext{ }%text{ }10^9)]text{ }%text{ }10^9
(a×b) % 109=[(a % 109)×(b % 109)] % 109

Tuy nhiên, nếu như ta cần lấy số dư cho 101810^{18}1018 thì sao? Phép toán bằng tính chất phân phối bây giờ sẽ không thể thực hiện được, vì [(a % 1018)×(b % 1018)]≤1036,[(atext{ }%text{ }10^{18})times(btext{ }%text{ }10^{18})]le10^{36},[(a % 1018)×(b % 1018)]≤1036, dẫn đến kết quả của bước này sẽ bị vượt quá khả năng biểu diễn của kiểu số nguyên $64$ bit.

Phép nhân Ấn Độ sử dụng để tính $(a\times b)\%M$ trong trường hợp tính chất phân phối với phép đồng dư thức không thể áp dụng được vì lí do tràn số.

2. Phép nhân Ấn Độ với đồng dư thức

Nguyên lí phép nhân Ấn Độ rất đơn giản như sau:

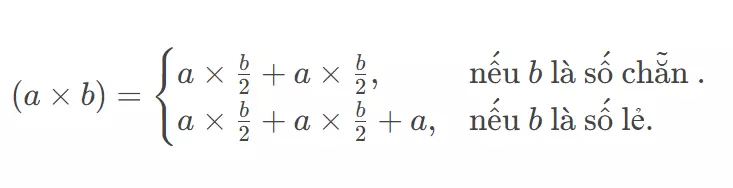
Dựa trên lý thuyết này, ta sẽ kết hợp phép nhân Ấn Độ với tính chất phân phối của phép nhân với phép đồng dư thức để tính được $(a\times b)\%M$, với M≤1018M le 10^{18}M≤1018 mà không bị tràn số. Dưới đây là cài đặt sử dụng giải thuật chia để trị, áp dụng đệ quy:

longlongmultiply_modulo(longlong A,longlong B,longlong M){if(B ==0)return0;longlong T =multiply_modulo(A, B /2, M)% M;if(B &1)return((T + T)% M + A % M)% M;elsereturn(T + T)% M;}intmain(){int A, B, M;
    cin >> A >> B >> M;

    cout <<multiply_modulo(A, B, M);}

Đánh giá độ phức tạp: Ở mỗi lần gọi đệ quy, $B$ giảm đi một nửa, nên độ phức tạp của giải thuật là O(log⁡2(B))O(log_2(B))O(log2​(B)).

V. Lũy thừa Modulo

1. Giải thuật chia để trị

Dựa trên tư tưởng phép nhân Ấn Độ, ta có thể điều chỉnh công thức một chút để tính được lũy thừa ab %M,a^b %M,ab %M, với a,b,M≤109a, b, M le 10^9a,b,M≤109. Công thức đơn giản như sau:

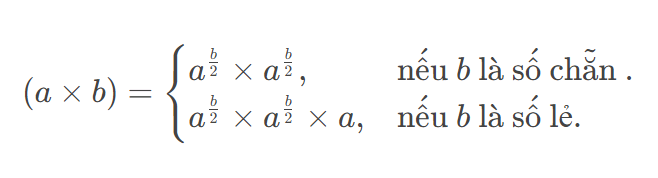
Cài đặt:

intpower_modulo(int A,int B,int M)// Tính A^B % M, {if(B ==0)return1LL;int half =power_modulo(A, B /2, M)% M;if(B &1)return(half * half * A)% M;elsereturn(half * half)% M;}

Đánh giá độ phức tạp: Ở mỗi lần gọi đệ quy, $B$ giảm đi một nửa, nên độ phức tạp của giải thuật là O(log⁡2(B))O(log_2(B))O(log2​(B)).

2. Tính AB % MA^Btext{ }%text{ }MAB % M với M≤1018M le 10^{18}M≤1018

Trong trường hợp M≤1018M le 10^{18}M≤1018, dựa trên những gì đã phân tích ở phần I, phép nhân thông thường sẽ không thể áp dụng vì lí do xảy ra tràn số. Vì vậy, ta sẽ kết hợp thêm phép nhân Ấn Độ trong trường hợp này. Độ phức tạp sẽ trở thành O(log⁡2(B)2)O(log_2(B)^2)O(log2​(B)2)

Cài đặt:

longlongpower_modulo(longlong A,longlong B,longlong M){if(B ==0)return1LL;int half =power_modulo(A, B /2LL, M)% M;
    half =multiply_modulo(half, half, M);if(B &1)returnmultiply_modulo(half, A, M);elsereturn half;}

3. Tính AB % MA^B % MAB % M trong trường hợp $B$ là số lớn và $M$ là số nguyên tố:

Đối với các trường hợp $B$ là số lớn – hiểu là các số nằm ngoài khả năng lưu trữ của kiểu số trong C++ và phải lưu bằng kiểu chuỗi – khi đó giải thuật tính AB % MA^B % MAB % M sẽ trở nên hơi phức tạp nếu như chúng ta cài đặt bằng các phép toán số lớn. Tuy nhiên, trong trường hợp $M$ là một số nguyên tố, dựa vào một số tính chất số học, ta có thể thu gọn được việc tính toán như sau:

• Thứ nhất, ta biết định lý nhỏ Fermat được phát biểu như sau: Nếu $M$ là một số nguyên tố thì:

  

• Lại có: AB % M=(AM−1.AM−1…AM−1.AX) % M,A^B % M = (A^{M-1}.A^{M-1}…A^{M-1}.A^X) % M,AB % M=(AM−1.AM−1...AM−1.AX) % M, với AM−1A^{M-1}AM−1 lặp lại ⌊BM−1⌋left lfloor{frac{B}{M-1}} right rfloor⌊M−1B​⌋ lần và $X=B\%(M-1)$. Từ đây suy ra:

  

Tới đây chúng ta có thể áp dụng lũy thừa modulo một cách bình thường mà không sợ bị tràn số. Tất nhiên vẫn sẽ cần lưu ý về giới hạn của $M$ để lựa chọn phép nhân thông thường hay phép nhân Ấn Độ. Việc cài đặt xin dành lại cho bạn đọc.

Tài liệu tham khảo:

• https://cowboycoder.tech/article/phep-nhan-an-do-va-phep-tinh-luy-thua
• https://vnoi.info/wiki/translate/he/Number-Theory-3.md