Tại sao cần Binary Search Trees?
Trong các phần trước, chúng ta đã thảo luận về các cách biểu diễn cây khác nhau và trong tất cả chúng, chúng ta không áp đặt bất kỳ hạn chế nào đối với dữ liệu trong node. Do đó, để tìm kiếm một phần tử, chúng ta cần kiểm tra cả cây con bên trái và cây con bên phải. Do đó, độ phức tạp trong trường hợp xấu nhất của thao tác tìm kiếm là O(n).
Trong phần này, chúng ta sẽ thảo luận về một biến thể khác của cây nhị phân: Cây tìm kiếm nhị phân (BST). Như tên gợi ý, công dụng chính của biểu diễn này là để tìm kiếm. Trong biểu diễn này, chúng ta áp đặt hạn chế đối với loại dữ liệu mà một node có thể chứa. Trong biểu diễn này, chúng ta áp đặt hạn chế đối với loại dữ liệu mà một node có thể chứa. Kết quả là, nó giảm thao tác tìm kiếm trung bình trong trường hợp xấu nhất xuống O(logn).
Các tính chất của Binary Search Trees
Trong cây tìm kiếm nhị phân, tất cả các phần tử của cây con bên trái phải nhỏ hơn dữ liệu gốc và tất cả các phần tử của cây con bên phải phải lớn hơn dữ liệu gốc. Đây được gọi là thuộc tính cây tìm kiếm nhị phân. Lưu ý rằng, thuộc tính này phải được thỏa mãn tại mọi node trong cây.
- Cây con bên trái của một node chỉ chứa các node có data nhỏ hơn node.
- Cây con bên phải của một node chỉ chứa các node có data lớn hơn node.
- Cả cây con bên trái và bên phải cũng phải là cây tìm kiếm nhị phân.
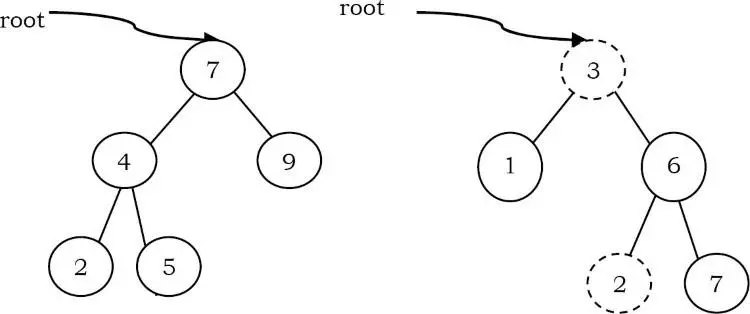
Ví dụ: Cây bên trái là cây tìm kiếm nhị phân và cây bên phải không phải là cây tìm kiếm nhị phân (tại node 6, nó không thỏa mãn thuộc tính của cây tìm kiếm nhị phân).
Khai báo cây tìm kiếm nhị phân
Không có sự khác biệt giữa khai báo cây nhị phân thông thường và khai báo cây nhị phân tìm kiếm. Sự khác biệt chỉ ở dữ liệu chứ không phải ở cấu trúc. Nhưng để thuận tiện, chúng ta đổi tên cấu trúc thành:
public class BinarySearchTreeNode {
private int data;
private BinarySearchTreeNode left;
private BinarySearchTreeNode right;
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public BinarySearchTreeNode getLeft() {
return left;
}
public void setLeft(BinarySearchTreeNode left) {
this.left = left;
}
public BinarySearchTreeNode getRight() {
return right;
}
public void setRight(BinarySearchTreeNode right) {
this.right = right;
}
}
Thao tác trên cây tìm kiếm nhị phân
Các thao tác chính
Các hoạt động chính được hỗ trợ bởi cây tìm kiếm nhị phân:
- Tìm/Tìm tối thiểu/Tìm tối đa trong cây tìm kiếm nhị phân
- Chèn một phần tử vào cây tìm kiếm nhị phân
- Xóa một phần tử khỏi cây tìm kiếm nhị phân
Hoạt động phụ trợ
- Kiểm tra xem cây đã cho có phải là cây tìm kiếm nhị phân hay không
- Tìm phần tử nhỏ thứ k trong cây
- Sắp xếp các phần tử của cây tìm kiếm nhị phân và nhiều hơn nữa
Notes về cây tìm kiếm nhị phân
- Vì dữ liệu gốc luôn nằm giữa dữ liệu cây con bên trái và dữ liệu cây con bên phải, nên việc thực hiện duyệt theo inorder traversal cây tìm kiếm nhị phân sẽ tạo ra một danh sách được sắp xếp.
- Trong khi giải các bài toán trên cây tìm kiếm nhị phân, đầu tiên chúng ta xử lý cây con bên trái, sau đó dữ liệu gốc và cuối cùng chúng ta xử lý cây con bên phải. Điều này có nghĩa là, tùy thuộc vào vấn đề, chỉ có bước trung gian (xử lý dữ liệu gốc) thay đổi và chúng ta không chạm vào bước đầu tiên và bước thứ ba.
- Nếu chúng ta đang tìm kiếm một phần tử và nếu dữ liệu gốc của cây con bên trái nhỏ hơn phần tử mà chúng ta muốn tìm kiếm thì hãy bỏ qua nó. Điều tương tự cũng xảy ra với cây con bên phải. Do đó, cây nhị phân tìm kiếm mất ít thời gian hơn để tìm kiếm một phần tử so với cây nhị phân thông thường. Nói cách khác, cây tìm kiếm nhị phân xem xét các cây con bên trái hoặc bên phải để tìm kiếm một phần tử chứ không phải cả hai.
- Các thao tác cơ bản có thể được thực hiện trên cây tìm kiếm nhị phân (BST) là chèn phần tử, xóa phần tử và tìm kiếm phần tử. Trong khi thực hiện các thao tác này trên BST, chiều cao của cây sẽ thay đổi mỗi lần. Do đó tồn tại các biến thể về độ phức tạp thời gian của trường hợp tốt nhất, trường hợp trung bình và trường hợp xấu nhất.
- Các hoạt động cơ bản trên cây tìm kiếm nhị phân mất thời gian tỷ lệ thuận với chiều cao của cây. Đối với một cây nhị phân hoàn chỉnh với n node, các hoạt động như vậy chạy trong trường hợp xấu nhất là O(lgn). Tuy nhiên, nếu cây là một chuỗi tuyến tính gồm n node (cây xiên), thì các thao tác tương tự sẽ mất O(n) thời gian trong trường hợp xấu nhất.
Tìm phần tử trong cây tìm kiếm nhị phân
Thao tác tìm rất đơn giản trong BST. Bắt đầu với thư mục gốc và tiếp tục di chuyển sang trái hoặc phải bằng thuộc tính của BST. Nếu dữ liệu chúng ta đang tìm kiếm giống với dữ liệu node thì chúng ta trả về node hiện tại. Nếu dữ liệu chúng ta đang tìm kiếm nhỏ hơn dữ liệu node thì tìm kiếm cây con bên trái của node hiện tại; mặt khác tìm kiếm cây con bên phải của node hiện tại. Nếu không có dữ liệu, chúng ta sẽ return null link.
public BinarySearchTreeNode find(BinarySearchTreeNode root, int data){
if(root == null){
return null;
}
if(data < root.getData()){
return find(root.getLeft(), data);
} else if (data > root.getData()) {
return find(root.getRight(), data);
}
return root;
}
Time Complexity: O(n), trong trường hợp xấu nhất (khi cây tìm kiếm nhị phân đã cho là cây nghiêng).
Space Complexity: O(n), dành cho ngăn xếp đệ quy.
Phiên bản non recursive của thuật toán trên có thể là:
public BinarySearchTreeNode find(BinarySearchTreeNode root, int data) {
if(root == null){
return null;
}
while(root != null){
if(data == root.getData()){
return root;
} else if (data > root.getData()) {
root = root.getRight();
} else {
root = root.getLeft();
}
}
return null;
}
Time Complexity: O(n). Space Complexity: O(1).
Tìm phần tử nhỏ nhất trong cây tìm kiếm nhị phân
Trong các BST, phần tử nhỏ nhất là node ngoài cùng bên trái mà không có node con bên trái. Trong BST bên dưới, phần tử tối thiểu là 4.

public BinarySearchTreeNode findMin(BinarySearchTreeNode root){
if(root == null){
return null;
} else{
if(root.getLeft() == null){
return root;
} else{
return findMin(root.getLeft());
}
}
}
Time Complexity: O(n), trong trường hợp xấu nhất (khi BST là cây lệch trái).
Space Complexity: O(n), đối với ngăn xếp đệ quy.
Phiên bản non recursive của thuật toán trên có thể là:
public BinarySearchTreeNode findMin(BinarySearchTreeNode root) {
if (root == null) {
return null;
}
while(root.getLeft() != null){
root = root.getLeft();
}
return root;
}
Time Complexity: O(n). Space Complexity: O(1).
Tìm phần tử lớn nhất trong cây tìm kiếm nhị phân
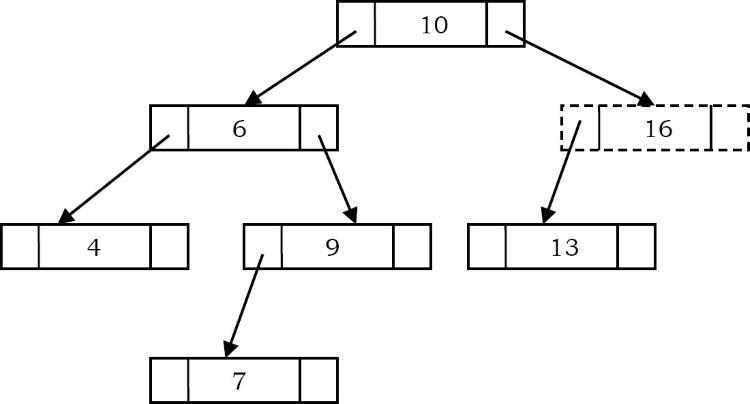
Trong các BST, phần tử lớn nhất là node ngoài cùng bên phải, không có node con bên phải. Trong BST bên dưới, phần tử tối đa là 16.
public BinarySearchTreeNode findMax(BinarySearchTreeNode root){
if(root == null){
return null;
} else{
if(root.getRight() == null){
return root;
} else{
return findMax(root.getRight());
}
}
}
Time Complexity: O(n), trong trường hợp xấu nhất (khi BST là cây lệch trái).
Space Complexity: O(n), đối với ngăn xếp đệ quy.
Phiên bản non recursive của thuật toán trên có thể là:
public BinarySearchTreeNode findMax(BinarySearchTreeNode root) {
if (root == null) {
return null;
}
while(root.getRight() != null){
root = root.getRight();
}
return root;
}
Time Complexity: O(n). Space Complexity: O(1).
Inorder Predecessor và Successor ở đâu?
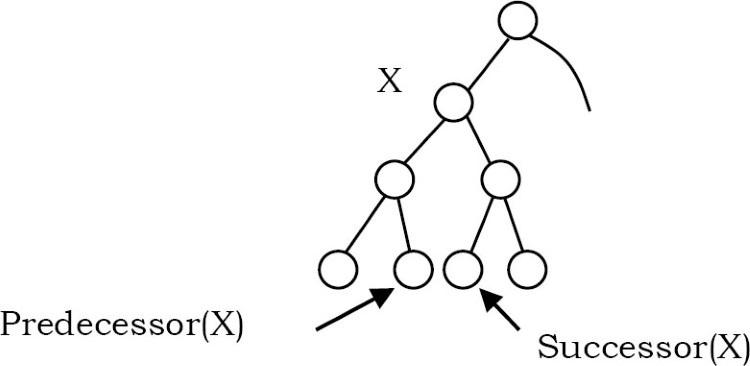
Đâu là Inorder Predecessor(tiền nhiệm) và Successor(kế nhiệm) của node X trong cây tìm kiếm nhị phân giả sử tất cả các node là khác nhau?
Nếu X có hai node con thì inorder predecessor của nó là giá trị lớn nhất trong cây con bên trái của nó và giá trị kế tiếp thứ tự của nó là giá trị nhỏ nhất trong cây con bên phải của nó.
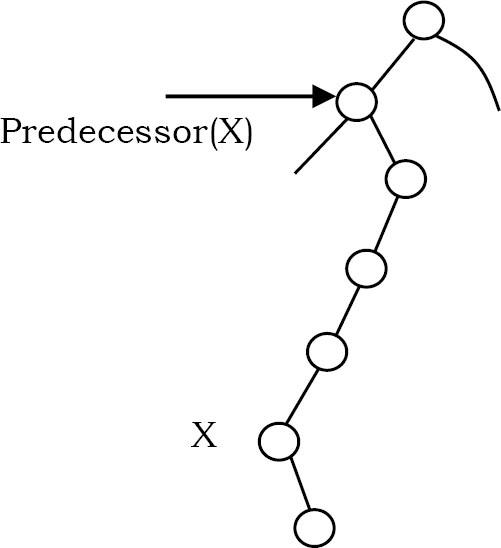
Nếu nó không có con bên trái, thì node inorder predecessor là tổ tiên bên trái đầu tiên của nó.
Chèn một phần tử từ cây tìm kiếm nhị phân
Để chèn dữ liệu vào cây tìm kiếm nhị phân, trước tiên chúng ta cần tìm vị trí cho phần tử đó. Chúng ta có thể tìm vị trí chèn bằng cách làm theo cơ chế tương tự như cơ chế của thao tác tìm. Trong khi tìm vị trí, nếu dữ liệu đã có ở đó thì chúng ta chỉ cần bỏ qua và đi ra. Nếu không, hãy chèn dữ liệu vào vị trí cuối cùng trên đường dẫn đi qua.
Như một ví dụ, chúng ta hãy xem xét cây sau đây. node chấm chấm cho biết phần tử (5) sẽ được chèn vào. node có các gạch đứt cho biết phần tử (5) sẽ được chèn vào. Để chèn 5, duyệt qua cây bằng chức năng tìm. Tại node có giá trị 4, chúng ta cần đi sang phải, nhưng không có cây con, vì vậy 5 không có trong cây và đây là vị trí chính xác để chèn.
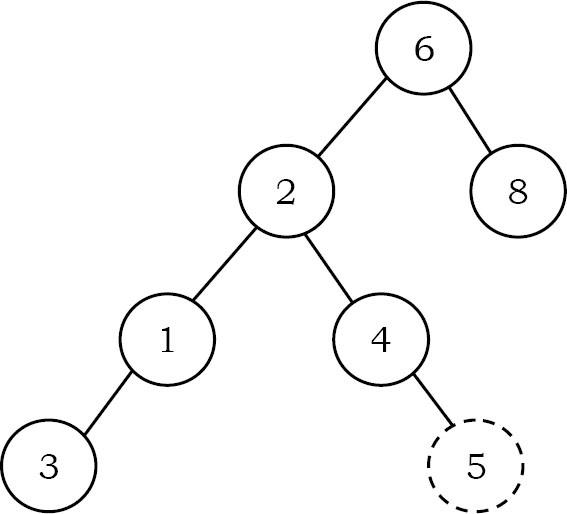
public BinarySearchTreeNode insert(BinarySearchTreeNode root, int data){
if(root == null){
root = new BinarySearchTreeNode();
if(root == null){
System.out.println("Memory error");
return null;
} else{
root.setData(data);
root.setLeft(null);
root.setRight(null);
}
} else {
if(data < root.getData()){
root.setLeft(insert(root.getLeft(), data));
} else if (data > root.getData()) {
root.setRight(insert(root.getRight(), data));
}
}
return root;
}
Lưu ý: Trong đoạn mã trên, sau khi chèn một phần tử vào cây con, cây được trả về node cha của nó.
Time Complexity: O(n).
Space Complexity: O(n), cho ngăn xếp đệ quy. Nếu sử dụng vòng lặp, space complexity là O(1).
Xóa một phần tử khỏi cây tìm kiếm nhị phân
Thao tác xóa phức tạp hơn các thao tác khác. Điều này là do phần tử bị xóa có thể không phải là node lá. Trong thao tác này cũng vậy, trước tiên chúng ta cần tìm vị trí của phần tử mà chúng ta muốn xóa. Khi chúng ta đã tìm thấy node bị xóa, hãy xem xét các trường hợp sau:
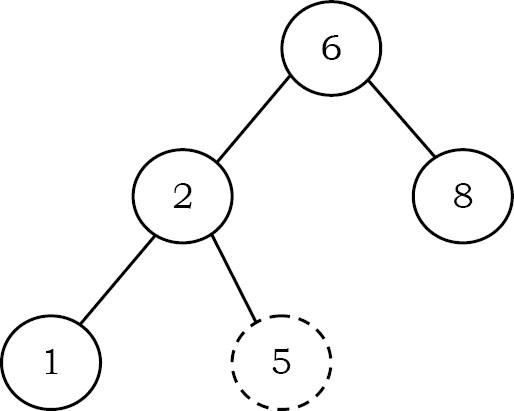
- Nếu phần tử cần xóa là node lá: trả lại NULL cho cha mẹ của nó. Điều đó có nghĩa là tạo con trỏ con tương ứng NULL. Trong cây bên dưới để xóa 5, đặt NULL thành node cha của nó là 2.
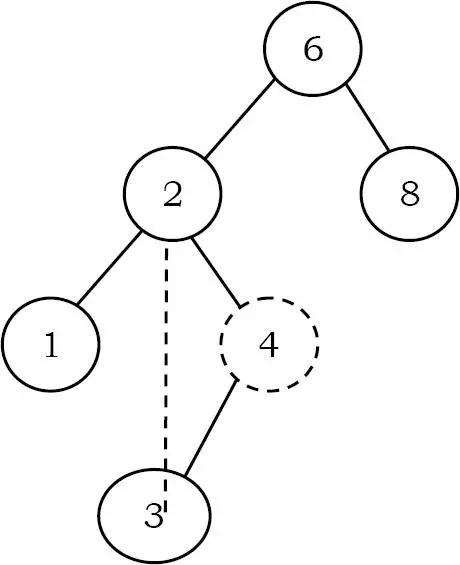
- Nếu phần tử bị xóa có một node con: Trong trường hợp này, chúng ta chỉ cần link node con của node hiện tại cho node cha của nó. Trong cây bên dưới, để xóa 4, cây con bên trái 4 được đặt thành node cha của nó là 2.
- Nếu phần tử bị xóa có cả hai phần tử con: Chiến lược chung là thay thế giá trị của node này bằng phần tử lớn nhất của cây con bên trái và xóa node đó đi. node lớn nhất trong cây con bên trái không thể có node con bên phải, vì vậy thao tác xóa thứ hai là dễ dàng. Ví dụ, chúng ta hãy xem xét cây sau đây. Trong cây dưới đây, để xóa 8, nó là con bên phải của gốc. Giá trị chính là 8. Nó được thay thế bằng giá trị lớn nhất trong cây con bên trái của nó (7), và sau đó node đó bị xóa như trước (trường hợp thứ hai).
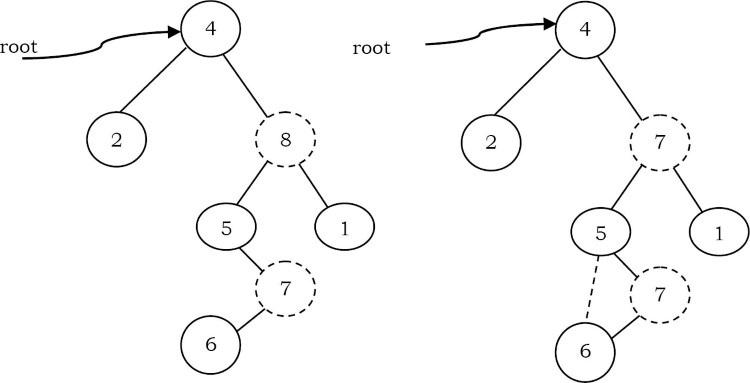
Lưu ý: Chúng ta cũng có thể thay thế bằng phần tử tối thiểu trong cây con bên phải.
public BinarySearchTreeNode delete(BinarySearchTreeNode root, int data){
BinarySearchTreeNode temp;
if(root == null){
System.out.println("Element not there in tree");
} else if (data < root.getData()) {
root.setLeft(delete(root.getLeft(), data));
} else if (data > root.getData()) {
root.setRight(delete(root.getRight(), data));
} else{ // Found element
if(root.getLeft() != null && root.getRight() != null){
// Replace with largest in left subtree
temp = findMax(root.getLeft());
root.setData(temp.getData());
root.setLeft(delete(root.getLeft(), root.getData()));
} else{ //One child
if(root.getLeft() == null){
root = root.getRight();
}
if(root.getRight() == null){
root = root.getLeft();
}
}
}
return root;
}
Time Complexity: O(n).
Space Complexity: O(n), cho ngăn xếp đệ quy. Nếu sử dụng vòng lặp, space complexity là O(1).
Nguồn: viblo.asia
