Chương 6: TREES – 3.Binary Trees: Problems & Solutions(27-40)

Problem-27

Đưa ra một thuật toán để chuyển đổi một cái cây thành gương của nó.
Gương của một cây là một cây khác với các nút con trái và phải của tất cả các nút không phải là lá được hoán đổi cho nhau.
2 cây trong ví dụ dưới đây là tấm gương phản chiếu lẫn nhau.

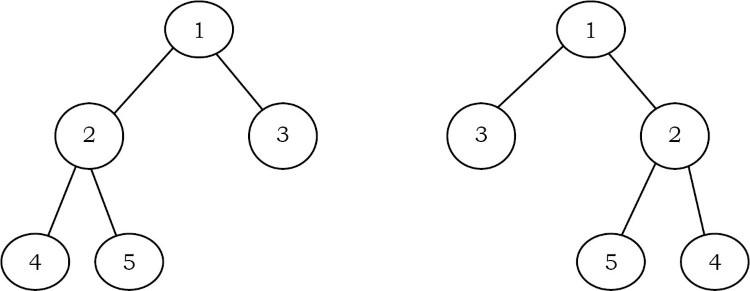
Solution:

	public BinaryTreeNode mirrorOfBinaryTree(BinaryTreeNode root) {
		BinaryTreeNode temp;
		if(root != null) {
			mirrorOfBinaryTree(root.left);
			mirrorOfBinaryTree(root.right);
			// swap the pointers in this node
			temp = root.left;
			root.left = root.right;
			root.right = temp;
		}
		return root;
	}

Time Complexity: O(n). Space Complexity: O(n).

Problem-28

Cho hai cây, hãy đưa ra thuật toán để kiểm tra xem chúng có phải là gương của nhau hay không.

Solution:

	public boolean areMirrors(BinaryTreeNode root1, BinaryTreeNode root2) {
		if(root1 == null && root2 == null) {
			return true;
		}
		if(root1 == null || root2 == null) {
			return false;
		}
		if(root1.data != root2.data) {
			return false;
		} else {
			return areMirrors(root1.left, root2.right) && areMirrors(root1.right, root2.left);
		}
	}

Time Complexity: O(n). Space Complexity: O(n).

Problem-29

Đưa ra một thuật toán để xây dựng cây nhị phân từ các Inorder and Preorder traversals đã cho.

Solution: Hãy xem xét các cách duyệt cây dưới đây:

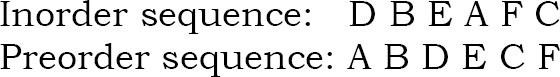
Trong trình tự Preorder, phần tử ngoài cùng bên trái biểu thị gốc của cây.
Vì vậy, chúng tôi biết ‘A’ là gốc của các chuỗi đã cho.
Bằng cách tìm kiếm ‘A’ trong Inorder, chúng ta có thể tìm ra tất cả các phần tử ở bên trái của ‘A’, nằm dưới cây con bên trái và các phần tử ở bên phải của ‘A’, nằm dưới cây con bên phải.
Vì vậy, chúng tôi nhận được cấu trúc như nhìn thấy dưới đây.

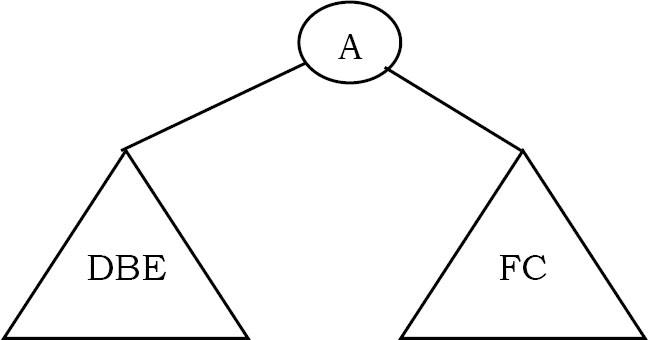
Chúng tôi đệ quy theo các bước trên và nhận được cây sau.

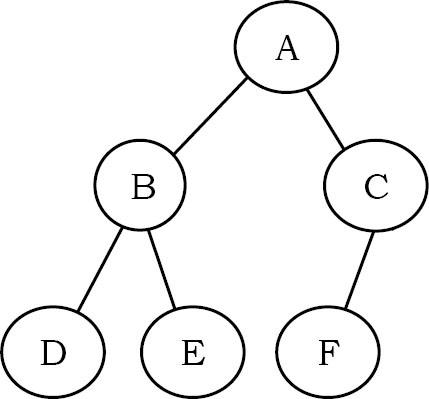
Algorithm: BuildTree()

1. Chọn một phần tử từ Preoder. Tăng biến Preorder index(xem mã ở dưới) để chọn phần tử tiếp theo trong lệnh gọi đệ quy tiếp theo.
2. Tạo một nút cây mới (newNode) với dữ liệu là phần tử được chọn.
3. Tìm index của phần tử đã chọn trong Inorder. Đặt index là inIndex.
4. Gọi BuildBinaryTree cho các phần tử trước inIndex và biến cây đã xây dựng thành cây con bên trái của newNode.
5. Gọi BuildBinaryTree cho các phần tử sau inIndex và biến cây đã xây dựng thành cây con bên phải của newNode.
6. return newNode.

Problem-30

Đưa ra thuật toán xây dựng cây nhị phân từ các phép duyệt Inorder và Postorder đã cho ở problem trên.

Solution:

public BinaryTreeNode buildBinaryTree(int[] inorder, int[] postOrder) {
		if(postOrder.length == 0 || postOrder.length != inorder.length) {
			return null;
		}
		return buildBT(postOrder, 0, postOrder.length - 1, inorder, 0, inorder.length - 1);
	}
	
	public BinaryTreeNode buildBT(int[] postOrder, int postStart, int postEnd, int[] inOrder, int inStart, int inEnd) {
		if(postStart > postEnd || inStart > inEnd) {
			return null;
		}
		int val = postOrder[postEnd];
		int offset = inStart;
		BinaryTreeNode cur = new BinaryTreeNode(val);
		// search for the inorder index
		for(; offset < inEnd; offset++) {
			if(inOrder[offset] == val) {
				break;
			}
		}
		cur.left = buildBT(postOrder, postStart, postStart + offset - inStart - 1, inOrder, inStart, offset - 1);
		cur.right = buildBT(postOrder, postStart + offset - inStart, postEnd - 1, inOrder, offset + 1, inEnd);
		return cur;
	}

Time Complexity: O(n). Space Complexity: O(1).

Problem-31

Nếu chúng ta được cung cấp hai traversal sequences, chúng ta có thể xây dựng cây nhị phân duy nhất không?

Solution: Nó phụ thuộc vào loại traversals nào được đưa ra. Nếu một trong các phương pháp traversal là Inorder thì cây có thể được xây dựng duy nhất, nếu không thì không thể.

Do đó, các kết hợp sau đây có thể xác định duy nhất một cây:

• Inorder và Preorder
• Inorder và Postorder
• Inorder và Level-order

Các kết hợp sau đây không xác định duy nhất một cây.

• Postorder và Preorder
• Preorder và Level-order
• Postorder và Level-order

Ví dụ, Preorder, Level-order và Postorder traversals giống nhau đối với các cây trên:
Preorder Traversal = AB
Postorder Traversal = BA
Level-order Traversal = AB

Vì vậy, ngay cả khi có ba trong số chúng (PreOrder, Level-Order và PostOrder) được đưa ra, cây không thể được xây dựng duy nhất.

Problem-32

Đưa ra thuật toán in ra tất cả các tổ tiên của một nút trong cây nhị phân. Đối với cái cây bên dưới, đối với 7 tổ tiên là 1 3 7.

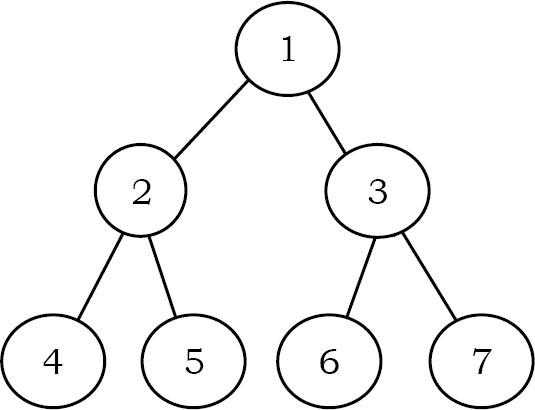
Solution:
Ngoài cách Depth First Search(Tìm kiếm theo chiều sâu) của cây này, chúng ta có thể sử dụng cách đệ quy sau để in ra các node tổ tiên.

	public static boolean printAllAncestors(BinaryTreeNode root, BinaryTreeNode node) {
		if(root == null) {
			return false;
		}
		if(root.left == node || root.right == node
				|| printAllAncestors(root.left, node) || printAllAncestors(root.right, node)) {
			System.out.println(root.data);
			return true;
		}
		return false;
	}

Time Complexity: O(n). Space Complexity: O(n) for recursion.

Problem-33

Đưa ra thuật toán tìm LCA (Least Common Ancestor – Tổ tiên chung gần nhất) của hai nút trong Cây nhị phân.

Solution:

	public BinaryTreeNode LCA(BinaryTreeNode root, BinaryTreeNode a, BinaryTreeNode b) {
		BinaryTreeNode left, right;
		if(root == null) {
			return root;
		}
		if(root == a || root == b) {
			return root;
		}
		
		left = LCA(root.left, a, b);
		right = LCA(root.right, a, b);
		
		if(left != null && right != null) {
			return root;	//nodes are each on a separate branch
		} else {
			return (left != null ? left : right);
			// either one node is on one branch, or none was found in any of the branches
		}
	}

Time Complexity: O(n). Space Complexity: O(n) for recursion.

Problem-34

Duyệt cây Zigzag: Đưa ra thuật toán duyệt cây nhị phân theo thứ tự Zigzag. Ví dụ: đầu ra cho cây bên dưới phải là: 1 3 2 4 5 6 7

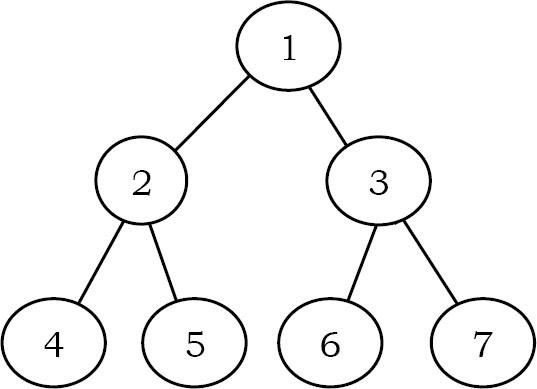
Solution:
Vấn đề này có thể được giải quyết dễ dàng bằng cách sử dụng hai ngăn xếp.
Giả sử hai ngăn xếp là: currentLevel và nextLevel.
Chúng tôi cũng sẽ cần một biến để theo dõi thứ tự level hiện tại (cho dù nó từ trái sang phải hay phải sang trái).
Chúng ta pop từ ngăn xếp currentLevel và in giá trị của node.
Bất cứ khi nào thứ tự current level là từ trái sang phải, hãy đẩy phần tử con bên trái của nút, sau đó là phần tử con bên phải của nó, để xếp nextLevel.
Vì ngăn xếp là cấu trúc Last In First Out (LIFO), nên lần tiếp theo các nút được pop khỏi nextLevel, nó sẽ theo thứ tự ngược lại.
Mặt khác, khi current level order là từ phải sang trái, chúng ta sẽ đẩy nút con phải của nút trước, sau đó là nút con trái của nó.
Cuối cùng, đừng quên hoán đổi hai ngăn xếp đó ở cuối mỗi cấp độ (ví dụ: khi currentLevel empty).

	public ArrayList<ArrayList<Integer>> zigzagLevelOrder(BinaryTreeNode root){
		ArrayList<ArrayList<Integer>> res = new ArrayList<>();
		if(root == null) {
			return res;
		}
		Queue<BinaryTreeNode> q = new LinkedList<>();
		q.offer(root);
		q.offer(null);
		boolean leftToRight = true;
		ArrayList<Integer> curr = new ArrayList<>();
		
		while(!q.isEmpty()) {
			BinaryTreeNode tmp = q.poll();
			if(tmp != null) {
				curr.add(tmp.data);
				if(tmp.left != null) {
					q.offer(tmp.left);
				}
				if(tmp.right != null) {
					q.offer(tmp.right);
				}
			} else {
				if(leftToRight) {
					 ArrayList<Integer> c_curr = new ArrayList<>(curr);
					 res.add(c_curr);
					 curr.clear();
				} else {
					Stack<Integer> s = new Stack<>();
					s.addAll(curr);
					ArrayList<Integer> c_curr = new ArrayList<>();
					while(!s.isEmpty()) {
						c_curr.add(s.pop());
					}
					res.add(c_curr);
					curr.clear();
				}
				if(!q.isEmpty()) {
					q.offer(null);
					leftToRight = !leftToRight;
				}
			}
		}
		return res;
	}

Time Complexity: O(n). Space Complexity: Space for two stacks = O(n) + O(n) = O(n).

Problem-35

Đưa ra thuật toán tìm tổng theo chiều dọc của cây nhị phân. Ví dụ,

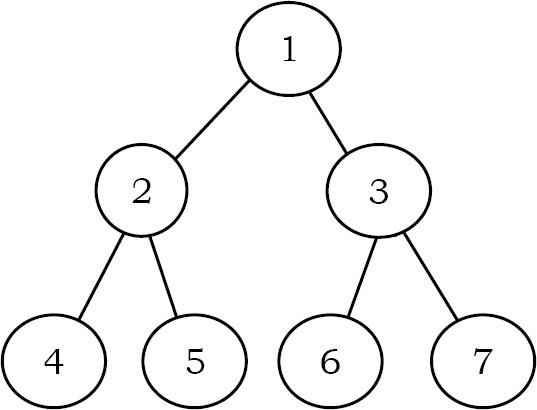
Cây có 5 đường vertical
Vertical-1: nodes-4 => vertical sum = 4
Vertical-2: nodes-2 => vertical sum = 2
Vertical-3: nodes-1,5,6 => vertical sum = 1 + 5 + 6 = 12
Vertical-4: nodes-3 => vertical sum = 3
Vertical-5: nodes-7 => vertical sum = 7
Ta cần output: 4 2 12 3 7

Solution:
Chúng ta có thể thực hiện inorder traversal và hash theo cột. Chúng ta gọi hàm VerticalSumInBinaryTree(root, 0) có nghĩa là root thì đang ở column 0. Trong khi thực hiện duyệt, hash theo cột và tăng giá trị của nó bằng root.getData()

	public static void vSum(HashMap<Integer, Integer> hash, BinaryTreeNode root, int c) {
		if(root.left != null) {
			vSum(hash, root.left, c-1);
		}
		if(root.right != null) {
			vSum(hash, root.right, c+1);
		}
		int data = 0;
		if(hash.containsKey(c)) {
			data = hash.get(c);
		}
		hash.put(c, root.data + data);
	}
	
	public static void verticalSum(BinaryTreeNode root) {
		HashMap<Integer, Integer> hash = new HashMap<>();
		vSum(hash, root, 0);
		System.out.println();
		for(int k : hash.keySet()) {
			System.out.println("key(pos): " + k + " sum: " + hash.get(k));
		}
	}

Problem-36

Có thể có bao nhiêu cây nhị phân khác nhau với n node?

Solution:

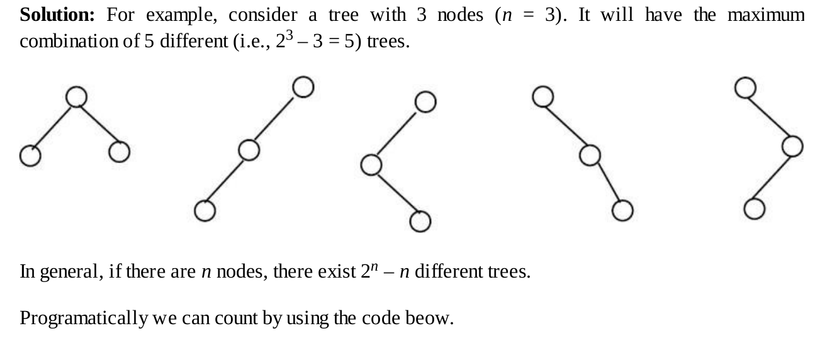
Trong sách tác giả viết công thức tổng quát là 2n−n2^n -n2n−n, nhưng mình thử với 4, 5, … thì không đúng lắm. Mn có thể tham khảo thêm ở đây hoặc ở đây

	public static int numOfBSTs(int n) {
		int[] count = new int[n+1];
		count[0] = 1;
		count[1] = 1;
		for(int i = 2; i <= n; i++) {
			for(int j = 0; j < i; j++) {
				count[i] += count[j] * count[i-j-1];
			}
		}
		return count[n];
	}

Time Complexity: O(n2)O(n^2)O(n2). Space Complexity: $O(n)$.

Problem-37

Đối với Problem-36, làm cách nào để tạo tất cả các BST khác nhau với n node?

Solution:

	public ArrayList<BinaryTreeNode> generateTrees(int n){
		if(n == 0) {
			return generateTrees(1, 0);
		}
		return generateTrees(1, n);
	}
	
	public ArrayList<BinaryTreeNode> generateTrees(int start, int end){
		ArrayList<BinaryTreeNode> subTrees = new ArrayList<>();
		if(start > end) {
			subTrees.add(null);
			return subTrees;
		}
		
		for(int i = start; i <= end; i++) {
			for(BinaryTreeNode left : generateTrees(start, i-1)) {
				for(BinaryTreeNode right : generateTrees(i+1, end)) {
					BinaryTreeNode aTree = new BinaryTreeNode(i);
					aTree.left = left;
					aTree.right = right;
					subTrees.add(aTree);
				}
			}
		}
		return subTrees;
	}

Problem-38

Cho một cây có thuộc tính đặc biệt trong đó các lá được biểu thị bằng ‘L’ và nút bên trong bằng ‘I’. Ngoài ra, giả sử rằng mỗi nút có 0 hoặc 2 nút con. Cho trước Preoder Traversal của cây này, hãy xây dựng cây. Ví dụ, Cho trước preoder string => ILILL

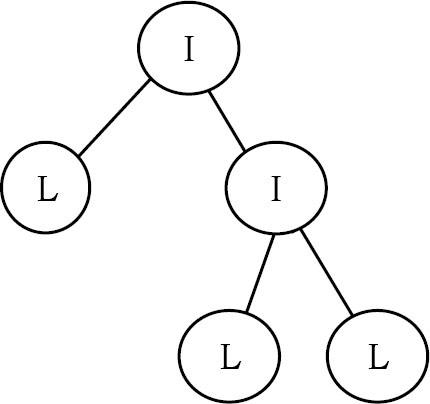
Solution:
Đầu tiên, chúng ta nên xem cách duyệt peroder được sắp xếp trước. Pre-order traversal nghĩa là trước tiên đặt nút gốc, sau đó duyệt trước theo thứ tự của cây con bên trái và sau đó duyệt theo thứ tự trước của cây con bên phải. Trong một kịch bản bình thường, không thể phát hiện nơi cây con bên trái kết thúc và cây con bên phải bắt đầu chỉ sử dụng pre-order traversal. Vì mỗi nút có 2 nút con hoặc không có nút con nào, nên chúng ta có thể chắc chắn rằng nếu một nút tồn tại thì anh chị em của nó cũng tồn tại. Vì vậy, mỗi khi tính toán một cây con, chúng ta cũng cần tính toán cây con anh em của nó.

Thứ hai, bất cứ khi nào chúng tôi nhận được ‘L’ trong chuỗi đầu vào, đó là một chiếc lá và chúng tôi có thể dừng lại cho một cây con cụ thể tại thời điểm đó. Sau nút ‘L’ này (con bên trái của cha mẹ ‘L’), cây anh chị em của nó bắt đầu. Nếu nút ‘L’ là con bên phải của nút cha, thì chúng ta cần đi lên trong cấu trúc phân cấp để tìm cây con tiếp theo để tính toán.

Lưu ý đến bất biến ở trên trong tâm trí, chúng ta có thể dễ dàng xác định khi nào một cây con kết thúc và cây con tiếp theo bắt đầu. Điều đó có nghĩa là chúng ta có thể cung cấp bất kỳ nút bắt đầu nào cho phương thức của mình và nó có thể dễ dàng hoàn thành cây con mà nó tạo ra bên ngoài các nút của nó. Chúng ta chỉ cần quan tâm đến việc chuyển các nút bắt đầu chính xác cho các cây con khác nhau.

	public BinaryTreeNode buildTreeFromPreOder(char[] A, int i) {
		if(A == null) {			//Boundary Condition
			return null;
		}
		if(A.length == i) {		//Boundary Condition
			return null;
		}
		
		BinaryTreeNode newNode = new BinaryTreeNode();
		newNode.setData(A[i]);
		newNode.setLeft(null);
		newNode.setRight(null);
		if(A[i] == 'L') {		//On reaching leaf node, return
			return newNode;
		}
		i++;
		newNode.setLeft(buildTreeFromPreOder(A, i));
		i++;
		newNode.setRight(buildTreeFromPreOder(A, i));
		
		return newNode;
	}

Problem-39

Cho một cây nhị phân có ba con trỏ (trái, phải và nextSibling), hãy đưa ra một thuật toán để điền vào các con trỏ nextSibling giả sử ban đầu chúng là NULL.

Solution: Một cách đơn giản chúng ta có thể sử dụng queue.

public class SiblingBinaryTreeNode {
	public int data;
	public SiblingBinaryTreeNode left;
	public SiblingBinaryTreeNode right;
	public SiblingBinaryTreeNode nextSibling;
	public SiblingBinaryTreeNode(int data) {
		this.data = data;
		left = null;
		right = null;
		nextSibling = null;
	}
	public SiblingBinaryTreeNode(int data, SiblingBinaryTreeNode left, SiblingBinaryTreeNode right,
			SiblingBinaryTreeNode nextSibling) {
		super();
		this.data = data;
		this.left = left;
		this.right = right;
		this.nextSibling = nextSibling;
	}
	public int getData() {
		return data;
	}
	public void setData(int data) {
		this.data = data;
	}
	public SiblingBinaryTreeNode getLeft() {
		return left;
	}
	public void setLeft(SiblingBinaryTreeNode left) {
		this.left = left;
	}
	public SiblingBinaryTreeNode getRight() {
		return right;
	}
	public void setRight(SiblingBinaryTreeNode right) {
		this.right = right;
	}
	public SiblingBinaryTreeNode getNextSibling() {
		return nextSibling;
	}
	public void setNextSibling(SiblingBinaryTreeNode nextSibling) {
		this.nextSibling = nextSibling;
	}
	
	public boolean isLeaf() {
		return left == null && right == null;
	}
	
}

	public void fillNextSiblings(SiblingBinaryTreeNode root){
		SiblingBinaryTreeNode tmp = null;
		if(root == null){
			return;
		}
		Queue<SiblingBinaryTreeNode> q = new LinkedList<>();
		q.offer(root);
		q.offer(null);
		while (!q.isEmpty()){
			tmp = q.poll();
			if(tmp != null){
				tmp.setNextSibling(q.peek());
				if (tmp.getLeft() != null) {
					q.offer(tmp.getLeft());
				}
				if (tmp.getRight() != null) {
					q.offer(tmp.getRight());
				}
			}else {
				// completion of a level
				if(!q.isEmpty()){
					q.offer(null);
				}
			}
		}
	}

Time Complexity: O(n). Space Complexity: O(n).

Problem-40

Có cách nào khác để giải quyết Problem-39 không

Solution: Bí quyết là sử dụng lại các con trỏ nextSibling đã điền. Như đã đề cập trước đó, chúng ta chỉ cần thêm một bước nữa để nó hoạt động. Trước khi chúng ta chuyển sang trái và phải cho chính hàm đệ quy, chúng ta kết nối nextSibling của nút con bên phải với nút con bên trái nextSibling của nút hiện tại. Để thuật toán này hoạt động, con trỏ nextSibling của nút hiện tại phải được điền, điều này đúng trong trường hợp này.

	public static void fillNextSiblings(SiblingBinaryTreeNode root){
		if(root == null){
			return;
		}
		if(root.getLeft() != null){
			root.getLeft().setNextSibling(root.getRight());
		}
		if(root.getRight() != null){
			if(root.getNextSibling() != null){
				root.getRight().setNextSibling(root.getNextSibling().getLeft());
			} else {
				root.getRight().setNextSibling(null);
			}
		}
		fillNextSiblings(root.getLeft());
		fillNextSiblings(root.getRight());
	}

Time Complexity: O(n).