[WRITE-UP] Cuộc thi An toàn thông tin – CTF – “WANNAGAME FRESHMAN 2022”

Intro

Chào mọi người, mình là Bích Sơn Nhật, sinh viên K17 thuộc khoa Công Nghệ Phần Mềm Trường Đại học Công nghệ Thông tin – ĐHQG TP.HCM. Dạo gần đây mình có tham gia cuộc thi CTF WANNAGAME FRESHMAN 2022 và đạt được thành tích với thứ hạng 29/59 đội với TeamBirthdayCake, thành viên gồm có bichsonnhat (bản thân mình). Các mảng bên cuộc thi rất đa dạng (𝐂𝐫𝐲𝐩𝐭𝐨𝐠𝐫𝐚𝐩𝐡𝐲, 𝐏𝐰𝐧𝐚𝐛𝐥𝐞, 𝐅𝐨𝐫𝐞𝐧𝐬𝐢𝐜/𝐌𝐢𝐬𝐜, …), nhưng mình không phải dân chuyên CTF nên chỉ quan tâm đến mảng 𝐏𝐫𝐨𝐠𝐫𝐚𝐦𝐦𝐢𝐧𝐠, và may mắn thay mình đã giải được 3 challenges trong vòng 2 ngày và đạt cả 3 FirstBlood. Hôm nay mình sẽ viết WriteUp cho Programming Challenge mà mình đã giải được gồm có : Threesum Problem, The Shortest Path, MITM.

Threesum Problem

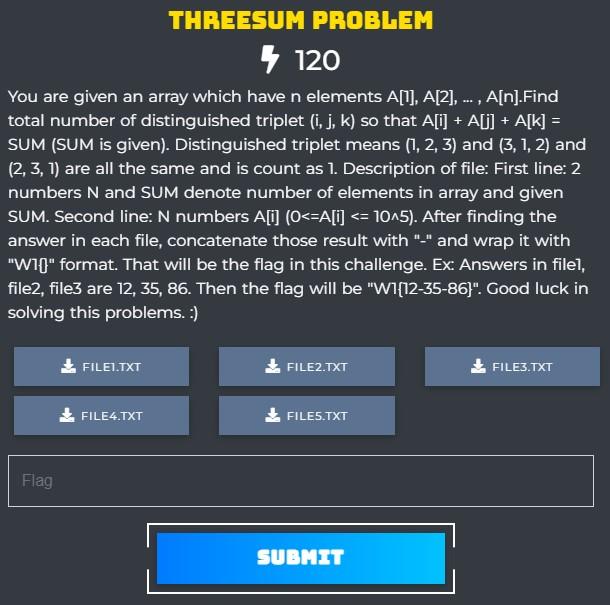
Đề bài: Cho một mảng gồm $n$ phần tử, đếm số cặp $(i,j,k)$ thoả mãn  ai+aj+ak=S ~a_i + a_j + a_k = S~ ai​+aj​+ak​=S 

Bài này lúc đầu mình cũng đắn đo giữ lắm, do tưởng giới hạn rất lớn, sau khi tải các test về thì mình check thì giới hạn chỉ có $n\le 3000$. Thì ý tưởng nảy ra ngay trong đầu mình là chặt nhị phân trên mảng để đếm kết quả, nhưng mà sau khi nghĩ lại thì mình quyết định BruteForce cho đỡ nghĩ 🙈

    /// C++ Solution Code
    
    int ans = 0;
    for (int i = 1; i + 2 <= n; ++i){
        for (int j = i + 1; j + 1 <= n; ++j){
             for (int k = j + 1; k <= n; ++k){
                 ans += (a[i] + a[j] + a[k] == S);
             }
         }
    }
    
    cout << ans << 'n';

The Shortest Path

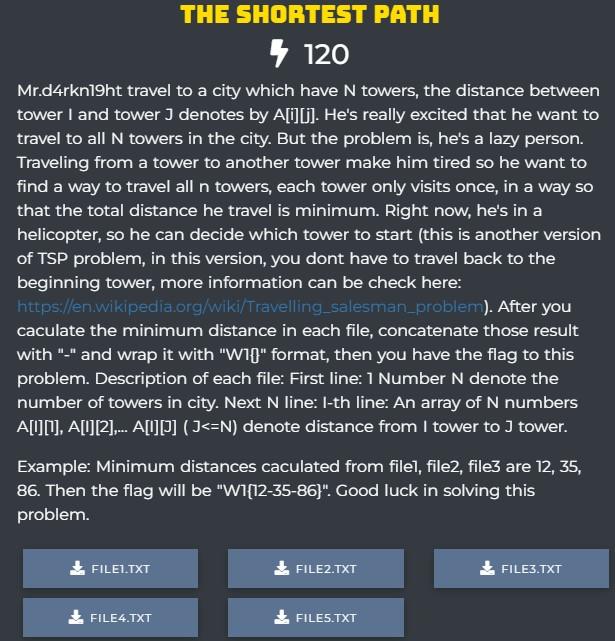
Đề bài: Cho một ma trận gồm $n\times n,n\le 20$ phần tử,  aij ~a_{ij}~ aij​  cho biết đường đi từ $i\to j$ tốn  aij ~a_{ij}~ aij​  đồng. Hãy tìm chi phí ít nhất để tham quan hết $n$ địa điểm, mỗi địa điểm đi qua đúng một lần. Lưu ý rằng bạn được phép xuất phát từ bất kì nơi nào để bắt đầu thực hiện di chuyển.

Thì thật ra Solution bài này đã có trong đề sẵn, đây là một dạng tương tự của TSP (Travelling Salesman Problem), thuật toán tối ưu nhất cho bài này là DP BitMask (Quy hoạch động Bitmask). Ban đầu mình chưa đọc kĩ ý sau, nên cứ tưởng là phải xuất phát từ địa điểm thứ $1$, và debug 2 giờ đồng hồ để phát hiện ra là mình đã đọc sai đề 😞. Để tiết kiệm thời gian, mình quyết định vét hết tất cả các địa điểm bằng cách hoán đổi 2 địa điểm $1$ và $i(2\le i\le n)$ cho nhau, điều này đồng nghĩa với việc mình phải làm mới lại ma trận sau khi hoán đổi.

    /// C++ Solution Swap 1 & k
     
    for (int k = 1; k <= 20; ++k){
 
        for (int i = 1; i <= n; ++i){
            for (int j = 1; j <= n; ++j){
                dist[i][j] = save[i][j];
            }
        }
 
        vector <int> a, b;
 
        for (int i = 1; i <= n; ++i){
            a.push_back(dist[1][i]);
            b.push_back(dist[k][i]);
        }
 
        for (int i = 0; i < n; ++i){
 
            if (i + 1 == 1 || i + 1 == k) continue;
            dist[k][i + 1] = a[i];
            dist[1][i + 1] = b[i];
        }
 
        dist[1][1] = dist[k][k] = 0;
 
        for (int i = 1; i <= n; ++i){
            if (i == 1 || i == k) continue;
            for (int j = 1; j <= n; ++j){
                dist[i][j] = dist[j][i];
            }
        }
 
        for (int i = 0; i <= n; ++i){
            for (int j = 0; j <= (1 << (n + 1)); ++j){
                memo[i][j] = 0;
            }
        }
 
        for (int i = 1; i <= n; ++i){
            ans = min(ans, dp(i, (1 << (n + 1)) - 1));
        }
 
    }

DP Bitmask Source Code:

long long dp(int i, int mask){
    if (mask == ((1 << i) | 3))
        return dist[1][i];
 
    if (memo[i][mask] != 0)
        return memo[i][mask];
 
    long long res = 1e18;
 
    for (int j = 1; j <= n; j++)
        if ((mask & (1 << j)))
            res = min(res, dp(j, mask & (~(1 << i))) + dist[j][i]);
    return memo[i][mask] = res;
}

MITM

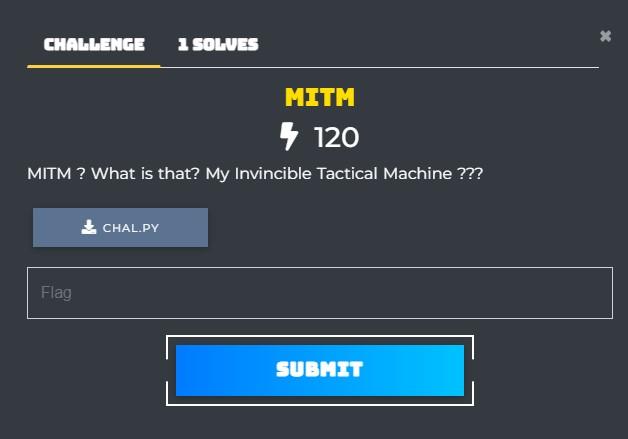
Ban đầu mình không định làm bài này đâu, do đọc không hiểu đề bài nói cái gì Nhưng sau khi hỏi author thì mình mới biết là phải tải file .py đó về rồi phân tích đề bài bằng source code đề cho.

Mình check thử xem file chứa gì:

MAXNUM = 10000000000000000
from random import randint
from secret import flag
from hashlib import sha256
def xor(a,b):
    return bytes([i^j for i,j in zip(a,b)])

arr = [randint(0, MAXNUM) for i in range(40)]
choice = [randint(0,1) for i in range(40)]
SUM = sum([i*j for i , j in zip(arr,choice)])
key = ''.join(str(i) for i in choice)
key = sha256(key.encode()).digest()

encrypt_flag = xor(flag.encode(), key)


print("Array :", arr)
print("Sum :", SUM)
#print(choice)
print("Encrypted flag :", encrypt_flag)
#print(xor(encrypt_flag, key))
# Array : [2598518492671225, 8179816363958449, 7404314384623807, 5036318129031785, 7561847828708907, 8810344945409856, 6802835477023830, 660775698577317, 6377835037958658, 5165653195950165, 5542182643266967, 8877017134340898, 7019762314080100, 5473217947093964, 5756053470367204, 6532571242263709, 9570025266332532, 7253491621003594, 570694512472223, 3928852819486391, 9419484349130866, 7231862012400760, 8471268887369720, 2064798807663638, 2463399225362608, 2933953912021332, 7404602394427554, 6864510477948829, 5953144542900222, 4727398111173660, 8953568444836994, 6186179598281467, 3950282663156437, 5074454322540355, 929515103368296, 2217898009467944, 7917815503532629, 2666540036871100, 1285546515475019, 6688163578190488]
# Sum : 86547527340532708
# Encrypted flag : b'3xeb$b@x8exa0Exc8Hx08xc0H3x054x0bxbcxb95x81xebxc1Rx97zxe0qNxe90N'

Đọc xong mình chả hiểu gì luôn, sau một hồi nghiên cứu thì mình đoán bài này có đề như sau:

Đề bài: Cho một dãy số nguyên gồm $n$ phần tử $(n\le 40)$ và số nguyên $Sum$, hãy tìm cách chọn các phần tử trong mảng để tổng cách phần tử đã chọn bằng $Sum$. Xuất ra mảng Choice có giá trị $[0,1]$

Sau khi đọc xong đề bài này thì ý tưởng Duyệt phân tập / Meet in the middle nảy ngay trong đầu và mình bắt tay vào code luôn.

Source Code Chia tập hợp

void Pre_Compute(long long a[], li arr[], int n, int id){
    for (int i = 0; i < (1 << n); ++i){
        long long sum = 0;
        for (int j = 0; j < n; ++j){
            if (i & (1 << j)) {
                sum += a[j + id];
                arr[i].second.push_back(j + id);
            }
        }
        arr[i].first = sum;
    }
}

Source Code tìm mảng Choice, vì đề yêu cầu mảng Choice có dạng $[0,1]$ nên mình sẽ xuất đáp án theo kiểu $0$ là không chọn, $1$ là chọn phần tử thứ $i$.

    Pre_Compute(a, x, n / 2, 0);
    Pre_Compute(a, y, n - n / 2, n / 2);
    int nx = 1 << (n / 2);
    int ny = 1 << (n - n / 2);
 
    sort(y, y + ny);
 
    int pos_x = -1, pos_y = -1;
 
    for (int i = 0; i < nx; ++i){
        long long cur = S - x[i].first;
 
        int l = 0, r = ny - 1;
 
        if (pos_y != -1) break;
 
        while (l <= r){
            int mid = (l + r) >> 1;
 
            long long cal = y[mid].first;
 
            if (cal == cur){
                pos_x = i; pos_y = mid;
                break;
            }
 
            if (cal < cur){
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
    }
 
    vector <bool> choice(n);
 
    for (auto &p : x[pos_x].second){
        choice[p] = true;
    }
 
    for (auto &p : y[pos_y].second){
        choice[p] = true;
    }
 
    for (int i = 0; i < n; ++i){
        cout << choice[i];
    }

Sau khi chạy test đề bài cho, mình được dãy đáp án như sau:

$1010000110011101011100001001100110110010$

Cuối cùng để tìm Flag, mình chỉ cần $XOR$keys vừa tìm được và encrypt_flag là xong:

from hashlib import sha256
def xor(a,b):
    return bytes([i^j for i,j in zip(a,b)])
    
keys = '1010000110011101011100001001100110110010'
keys = sha256(key.encode()).digest()

encrypt_flag = b'3xeb$b@x8exa0Exc8Hx08xc0H3x054x0bxbcxb95x81xebxc1Rx97zxe0qNxe90N'

print(xor(key, encrypt_flag))

Ta được Flag như hình:

Qua cuộc thi này mình đã rút ra nhiều bài học riêng cho bản thân và đúc kết nhiều kinh nghiệm cho các cuộc thi sắp tới.

Cảm ơn BTC Phòng thí nghiệm An toàn thông tin – UIT InSecLab đã tạo ra cuộc thi này dành cho tân sinh viên K17 có cơ hội trải nghiệm bản tân tại Trường Đại học Công nghệ Thông tin – ĐHQG TP.HCM.

Cảm ơn mọi người đã đọc.