1. Giới thiệu

Một thách thức quan trọng trong nhận dạng trực quan là làm thế nào để điều chỉnh các biến thể hình học hoặc mô hình hóa các biến đổi hình học về tỷ lệ đối tượng, tư thế, điểm nhìn và biến dạng bộ phận (Hình 1)

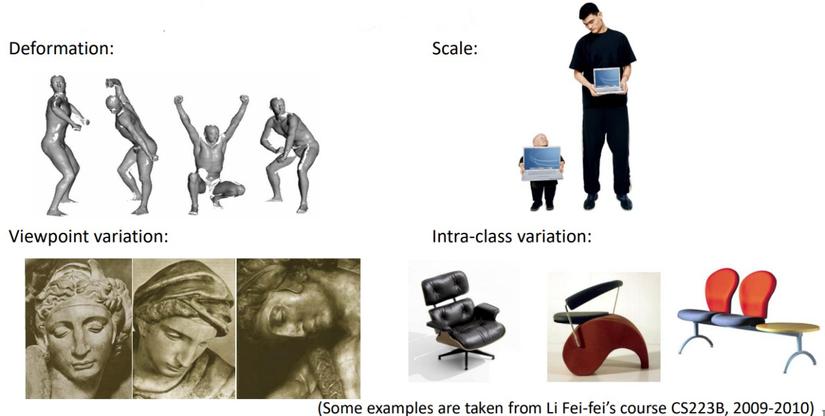
Hình 1: Một số vấn đề lâu dài trong thị giác máy tính Deformable Convolutional Networks pdf

Để giải quyết vấn đề này, phương pháp tiếp cận truyền thồng gồm 2 cách :

• Đầu tiên là xây dựng bộ dữ liệu đào tạo với đủ các biến thể mong muốn. Điều này thường được thực hiện bằng cách bổ sung các mẫu dữ liệu hiện có, ví dụ: bằng cách chuyển đổi affine. Các biểu diễn mạnh mẽ có thể được học từ dữ liệu, nhưng thường với chi phí đào tạo tốn kém và các tham số mô hình phức tạp. Bên cạnh đó, các phép biến đổi hình học được giả định là cố định và đã biết. Giả định này ngăn cản sự tổng quát hóa cho các nhiệm vụ mới sở hữu các phép biến đổi hình học chưa biết, không được mô hình hóa đúng.

• Thứ hai là sử dụng các tính năng và thuật toán biến đổi-bất biến (transformation-invariant). Danh mục này sử dụng nhiều kỹ thuật nổi tiếng, chẳng hạn như SIFT (scale invariant feature transform) và mô hình phát hiện đối tượng dựa trên cửa sổ trượt. Việc thiết kế thủ công các tính năng và thuật toán bất biến có thể khó hoặc không khả thi đối với các phép biến đổi quá phức tạp, ngay cả khi chúng đã được biết đến.

Mạng tích chập (Convolution Neural Network – CNN) rất phổ biến trong lĩnh vực thị giác máy tính và hầu hết các ứng dụng hiện đại như google images, xe tự lái, v.v. đều dựa trên chúng. Ở mức độ cao, chúng là tập trung vào thông tin không gian cục bộ và sử dụng trọng số để trích xuất các tính năng (features) theo cách phân cấp, cuối cùng được tổng hợp theo một số cách cụ thể cho từng tác vụ. Mặc dù CNN’s đã đạt được nhiều thành tựu cho các nhiệm vụ nhận dạng hình ảnh nhưng rất hạn chế khi nói đến việc mô hình hóa các biến thể hình học hoặc các phép biến đổi hình học. Phép biến đổi hình học là các phép biến đổi cơ bản biến đổi vị trí và hướng của một hình ảnh sang vị trí và hướng khác. Một số phép biến đổi hình học cơ bản là chia tỉ lệ, xoay, tịnh tiến, v.v. Mạng nơ-ron hình học thiếu cơ chế bên trong để tạo mô hình các biến thể hình học và chỉ có thể lập mô hình chúng bằng cách sử dụng các phép tăng cường dữ liệu được cố định và giới hạn bởi kiến thức của người dùng và do đó CNN không thể học các phép biến đổi hình học chưa biết đến người dùng.

Để khắc phục sự cố này và tăng khả năng của CNN, Deformable Convolutions (DCN) đã được giới thiệu bởi Microsoft Research Asia (MSRA). Nó cũng được gọi là DCNv1 vì sau này các tác giả cũng đề xuất DCNv2. Trong công việc của mình, họ đã giới thiệu một cơ chế đơn giản , hiệu quả và end-to-end giúp CNN có khả năng học các phép biến đổi hình học khác nhau theo dữ liệu đã cho.

2. Deformable Convolutional Networks

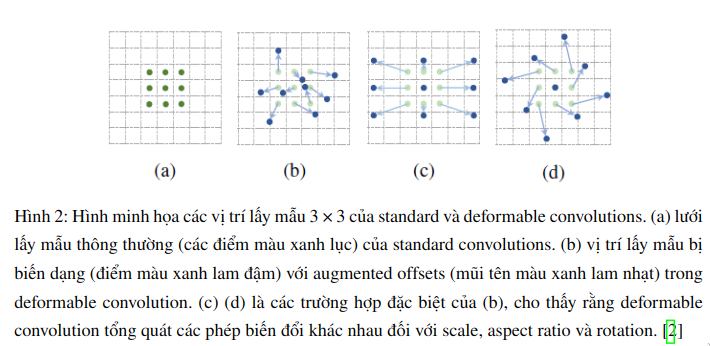
Trong bài báo này, nhóm tác giả giới thiệu hai mô-đun mới giúp nâng cao năng lực của CNN trong việc mô hình hóa các phép biến đổi hình học. Mô đun thử nhất tên là deformable convolution. Nó thêm một mảng offset 2D với các vị trí lấy mẫu lưới thông thường trong CNN truyền thống. Điều này cho phép lớp tích chập lấy mẫu tại những vị trí đa dạng hơn. Nó được minh họa trong Hình 2. Các offset được thêm vào có thể học được từ các bản đồ đặc trưng trước đó bằng cách sử dụng các lớp tích chập bổ sung. Do đó, các biến dạng này phụ thuộc vào các tính năng đầu vào một cách cục bộ, dày đặc và thích ứng.

Thứ hai là deformable RoI pooling. Nó thêm một offset đến từng vị trí bin trong phân vùng bin thông thường của RoI pooling trước đó. Tương tự, các offsets được học từ các bản đồ tính năng trước đó và RoIs, cho phép bản địa hóa phần thích ứng cho các đối tượng có hình dạng khác nhau.

Cả hai mô-đun đều có trọng lượng nhẹ. Chúng thêm một lượng nhỏ của các tham số và tính toán cho offset learning. Chúng có thể dễ dàng thay thế các đối tác đơn giản của chúng trong CNN sâu và có thể dễ dàng được đào tạo từ đầu đến cuối với việc lan truyền ngược tiêu chuẩn. Các CNNs đó có thể được gọi là deformable convolutional networks, hoặc deformable ConvNets

2.1 Deformable convolution

Để giải thích chi tiết về Deformable Convolutions, trước tiên ta sẽ thảo luận về Convolution truyền thống và sau đó giải thích ý tưởng đơn giản được thêm vào để chuyển đổi chúng thành deformable convolutions. Convolution truyền thống thường thực hiện theo 2 bước:

1. Lấy mẫu bằng cách sử dụng một lưới thông thường R trượt qua bản đồ đặc trưng đầu vào.
2. Tổng hợp các giá trị lấy mẫu có đánh trọng số bởi w (weight)

Ta sẽ giải thích hai khái niệm trên dưới dạng phương trình toán học. Gọi $\mathcal{R}$ là một kernel 3×3 được sử dụng để lấy mẫu một vùng nhỏ của bàn đổ đặc trưng đầu vào:

$$\mathcal{R}=\left\{(-1,-1),(-1,0),\dots (0,1),(1,)\right\}$$

Sau đó, phương trình của phép toán tích chập 2d thông thường như phương trình (1), trong đó $w$ là trọng số của kernel, $x$ là bản đồ đặc trưng đầu vào, $y$ là đầu ra của phép toán tích chập, p0p_{0}p0​ là vị trí bắt đầu của mỗi hạt nhân và pnp_{n}pn​ đang liệt kê cùng với tất cả các vị trí trong $\mathcal{R}$.

y(p0)=∑pn∈Rw(pn)⋅x(p0+pn)(1)y(p_{0}) = sum_{p_{n}in mathscr{R}} w(p_{n})cdot x(p_{0} + p_{n}) (1)
y(p0​)=pn​∈R∑​w(pn​)⋅x(p0​+pn​)(1)

Phương trình biểu thị phép toán tích chập trong đó mỗi vị trí trên lưới được lấy mẫu lần đầu tiên được nhân với giá trị tương ứng của ma trận trọng số và sau đó được tổng hợp để đưa ra kết quả vô hướng và lặp lại thao tác tương tự trên toàn bộ hình ảnh sẽ cho chúng ta bản đồ đặc trưng mới. Nếu $\mathcal{R}$ là lưới bình thường, thì phép toán Deformable Convolution tăng cường offsets đã học cho lưới, do đó làm biến dạng các vị trí lấy mẫu của lưới.

Phép toán Deformable Convolution có thể định dạng được mô tả bằng Phương trình (2), trong đó
{Δpn∣n=1,2,…,N}left{ Delta p_{n}|n =1,2,…,Nright}{Δpn​∣n=1,2,…,N} với $N=|\mathcal{R}|$ biểu thị các offset được thêm vào phép toán tích chập thông thường:

y(p0)=∑pn∈Rw(pn)⋅x(p0+pn+Δpn)(2)y(p_{0}) = sum_{p_{n}in mathscr{R}} w(p_{n})cdot x(p_{0} + p_{n} + Delta p_{n}) (2)
y(p0​)=pn​∈R∑​w(pn​)⋅x(p0​+pn​+Δpn​)(2)

Bây giờ khi việc lấy mẫu được thực hiện trên các vị trí không đều và lệch;ΔpnDelta p_{n}Δpn​ thường là phân số, các tác giả sử dụng nội suy song tuyến để thực hiện phương trình trên. Nội suy song tuyến được sử dụng vì khi thêm offset vào các vị trí lấy mẫu hiện có, chúng ta thu được các điểm phân số không phải là vị trí xác định trên lưới và để ước tính giá trị pixel của chúng, chúng tôi sử dụng nội suy song tuyến sử dụng lưới 2×2 của các giá trị pixel lân cận để ước tính giá trị pixel của vị trí bị biến dạng mới. Phương trình (3) thực hiện nội suy hai tuyến tính và ước tính giá trị pixel tại vị trí phân số, trong đó p=(p0+pn+Δpn)p = ( p_{0} + p_{n} + Delta p_{n})p=(p0​+pn​+Δpn​) là vị trí bị biến dạng, $q$ liệt kê tất cả các vị trí hợp lệ trên bản đồ đối tượng đầu vào và $G(..)$ là nhân nội suy song tuyến.

x(p)=∑qG(q,p)⋅x(q)(3)x(p) = sum_{q} G(q, p)cdot x(q) (3)
x(p)=q∑​G(q,p)⋅x(q)(3)

Lưu ý: $G$ là hai chiều. Nó được tách thành hai hạt nhân một chiều như sau:

G(q,p)=g(qx,px)⋅g(qy,py) G(q,p) = g(q_{x}, p_{x})cdot g(q_{y}, p_{y})
G(q,p)=g(qx​,px​)⋅g(qy​,py​)

trong đó $g(a,b)=max(0,1-|a-b|)$. Ta có thể đọc thêm 3 để hiểu rõ hơn về tính nội suy song song.

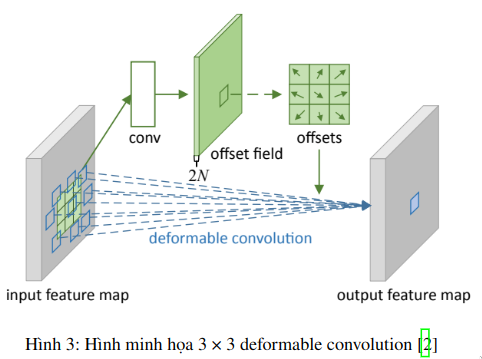
Như minh học Hình 3, offset thu được bằng cách áp dụng một lớp tích chập trên bản đồ tính năng đầu vào. Convolution kenel được sử dụng có độ phân giải và giãn nở không gian như của lớp tích chập hiện tại. Offset fields đầu ra có cùng độ phân giải với độ phân giải của bản đồ tính năng đầu vào và channel có kích thước channel 2N tương ứng với N 2D offsets. Trong quá trình đào tạo, cả hai convolutional kernels để tạo ra các tính năng đầu ra và các offset đều được học đồng thời.

2.2 Deformable RoI Pooling

RoI (Region of Interest) pooling rất hay được sử dụng trong gợi ý các vùng chứa đối tượng trong các bài toán object detection. Lớp pooling này giúp chuyển một vùng đầu vào có kích thước bất kì thành vùng đặc trưng có kích thước cố định.

2.2.1 RoI Pooling

Cho đầu vào một biểu đồ tính năng (input feature map) $x$, một RoI kích thước $w\times h$ và vùng top-left p0p_{0}p0​, RoI pooling chia RoI thành $k\times k$ ($k$ bất kỳ) bins và đầu ra một biểu đồ đặc trưng kích thước $k\times k$$y$. Với $(i,j)$-th bin ($0\le i,j<k$), ta có:

y(i,j)=∑p∈bin(i,j)x(p0+p)/nijy(i,j) = sum_{pin bin(i,j)} x(p_{0} + p)/n_{ij}
y(i,j)=p∈bin(i,j)∑​x(p0​+p)/nij​

Trong đó, nijn_{ij}nij​ là số lượng pixel trong bin đó, bin thứ $(i,j)$ kéo dài từ ⌊iwk⌋≤px<⌈(i+1)wk⌉lfloor itfrac{w}{k} rfloor leq p_{x} < lceil (i+1)tfrac{w}{k} rceil⌊ikw​⌋≤px​<⌈(i+1)kw​⌉ và ⌊ihk⌋≤py<⌈(i+1)hk+1⌉lfloor itfrac{h}{k} rfloor leq p_{y} < lceil (i+1)tfrac{h}{k+1} rceil⌊ikh​⌋≤py​<⌈(i+1)k+1h​⌉.

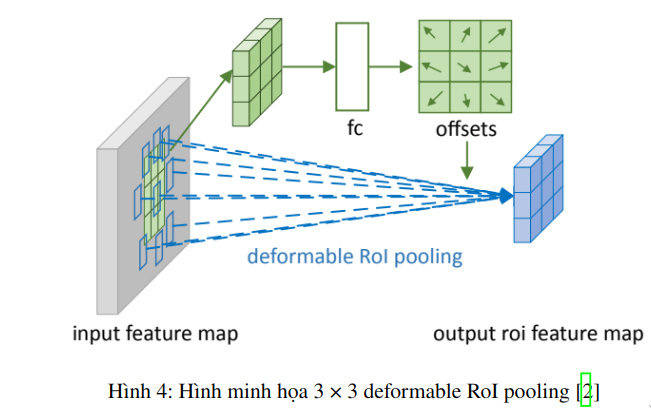
Tương tự như phương trình (2), trong deformable RoI pooling, offsets Δpij∣0≤i,j<k{Delta p_{ij} |0 ≤ i, j < k}Δpij​∣0≤i,j<k được thêm vào các vị trí trong không gian. Eq.(5) trở thành:

y(i,j)=∑p∈bin(i,j)x(p0+p+Δpij)/nijy(i,j) = sum_{pin bin(i,j)} x(p_{0} + p + Delta p_{ij})/n_{ij}
y(i,j)=p∈bin(i,j)∑​x(p0​+p+Δpij​)/nij​

Hình 4. minh họa làm thế nào để có được offsets. Đầu tiên, RoI pooling (Eq. 5) tạo ra polled features maps. Từ poolled features map, một lớp fully connect tạo ra normalized offsets Δp^i,jDelta hat{p}_{i,j}Δp^​i,j​. Sau đó, Δpi,j=γ⋅Δp^i,j∘(w,h)Delta p_{i,j} = gamma cdot Delta hat{p}_{i,j} circ (w, h)Δpi,j​=γ⋅Δp^​i,j​∘(w,h). Ở đây, $\gamma$ là một đại lượng vô hướng được xác định trước để điều chỉnh độ lớn của offsets. Theo kinh nghiệm, nó được đặt thành $\gamma =0,1$.

2.2.2 Position-Sensitive (PS) RoI Pooling

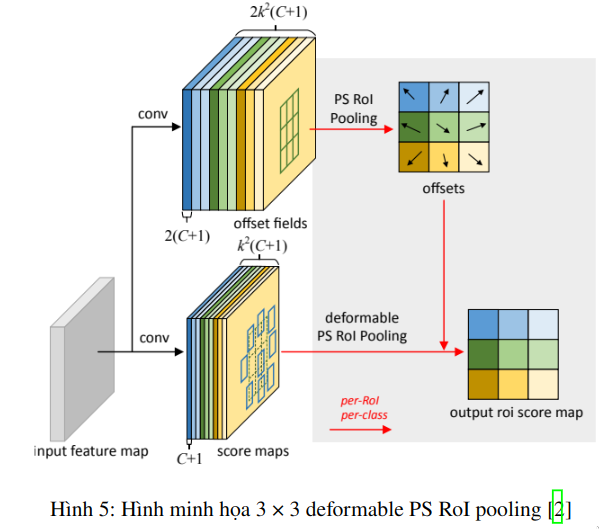
Đối với Positive-Sensitive (PS) RoI pooling ban đầu trong R-FCN , tất cả input feature map đầu trước hết được chuyển đổi thành bản k2k^{2}k2 score maps cho mỗi lớp đối tượng (Tổng cộng $C+1$ cho $C$ lớp đối tượng + 1 nền)

Trong deformable PS RoI pooling, trước tiên, ở đường dẫn trên cùng , tương tự như bản gốc, conv được sử dụng để tạo 2k2(C+1)2k^{2}(C +1)2k2(C+1) score maps. Điều đó có nghĩa là đối với mỗi lớp, sẽ có k2k^{2}k2 features maps. k2k^{2}k2 feature map này đại diện cho biểu diễn tọa độ 2 chiều của {top-left (TL), top-center (TC), .. , bottom right (BR)} của đối tượng mà chúng tôi muốn tìm hiểu offsets. Original PS RoI pooling cho offset (đường trên) được thực hiện theo nghĩa là chúng được gộp với cùng một khu vực và cùng màu như trong hình 5. Chúng tôi nhận được offsets ở đây. Cuối cùng, ở nhánh dưới trong hình 5} , chúng tôi thực hiện deformable PS RoI pooling để pool the feature maps được tăng cường bởi offsets.

2.3 Understanding Deformable ConvNets

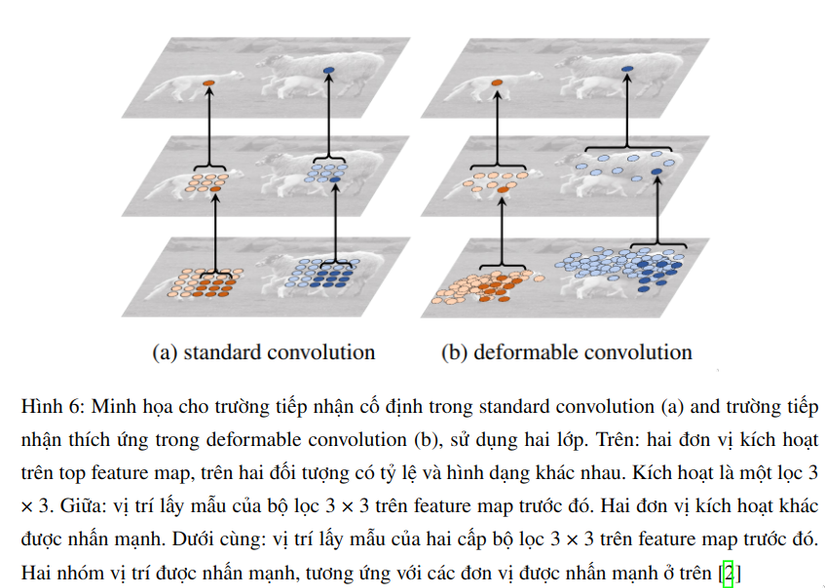
Bài báo được xây dựng dựa trên ý tưởng tăng cường các vị trí lấy mẫu không gian trong convolution và RoI pooling với các offset bổ sung và các offset được học hỏi từ các nhiệm vụ mục tiêu. Khi deformable convolution được xếp chồng lên nhau, ảnh hưởng của biến dạng tổng hợp là rất sâu sắc. Điều này được minh họa trong Hình 6. Trường tiếp nhận và các vị trí lấy mẫu trong standard convolution được cố định trên feature map trên cùng (bên trái). Chúng được điều chỉnh một cách thích ứng theo tỷ lệ và hình dạng của đối tượng trong deformable convolution (bên phải). Các ví dụ khác được thể hiện trong Hình 7.

Ảnh hưởng của deformable RoI pooling cũng tương tự, như được minh họa trong Hình 8. Tính ổn định của cấu trúc lưới trong standard RoI pooling không còn được giữ. Thay vào đó, các bộ phận sẽ lệch khỏi các RoI bins và di chuyển lên các vùng tiền cảnh của đối tượng gần đó. Khả năng bản địa hóa được nâng cao, đặc biệt là đối với các đối tượng không cứng (non-rigid).

Tổng kết

Trong bài viết này, mình đã trình bày deformable ConvNets, là một giải pháp đơn giản, hiệu quả, sâu và toàn diện để mô hình hóa các phép biến đổi không gian dày đặc, và khả năng tích hợp dễ dàng vào các mạng. Bài báo cho thấy rằng việc học chuyển đổi không gian dày đặc trong CNN là khả thi và hiệu quả cho các nhiệm vụ tầm nhìn phức tạp. Cảm ơn các bạn đã đọc hết bài viết, hẹn gặp lại các bạn trong các bài viết tiếp theo có thể là review version 2 .

Tài liệu tham khảo

1. Scale Invariant Feature Transform (SIFT)
2. Deformable Convolutional Networks
3. Review Deformable Convolution by Xiaohong
4. R-FCN: Object Detection via Region-based Fully Convolutional Networks
5. https://pub.towardsai.net/review-dcnv2-deformable-convnets-v2-object-detection-instance-segmentation-3d8a18bee2f5
6. Slide DCN
7. https://viblo.asia/p/so-luoc-ve-deformable-convolution-networks-ORNZqn0Ll0n#_21-deformable-convolution-4