1. Introduction
Đây là một giải thuật để tính ước chung lớn nhất (GCD – Greatest Common Divisor) của hai số nguyên, là số lớn nhất có thể chia được bởi hai số nguyên đó với số dư bằng không.
Thuật toán Euclidean cho hai số nguyên A và B được mô tả bằng các bước như sau:
- Nếu A = 0 thì GCD (A, B) = B, vì GCD (0, B) = B, và chúng ta có thể dừng lại.
- Nếu B = 0 thì GCD (A, B) = A, vì GCD (A, 0) = A, và chúng ta có thể dừng lại.
- Biểu diễn A dưới dạng phần dư và thương số (A = B⋅Q + R)
- Tìm GCD(B,R) sử dụng thuật toán Euclidean vì GCD(A,B) = GCD(B,R)
Ví dụ tìm ước chung lớn nhất của 38 và 16.
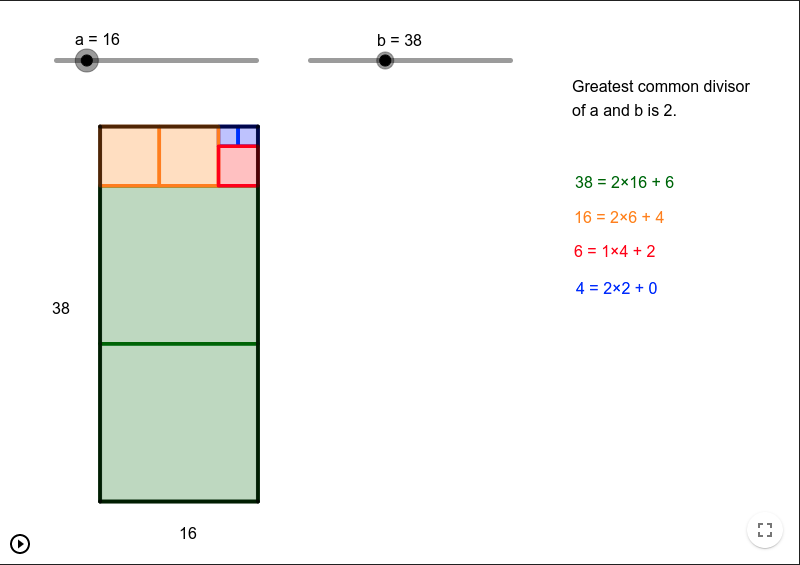
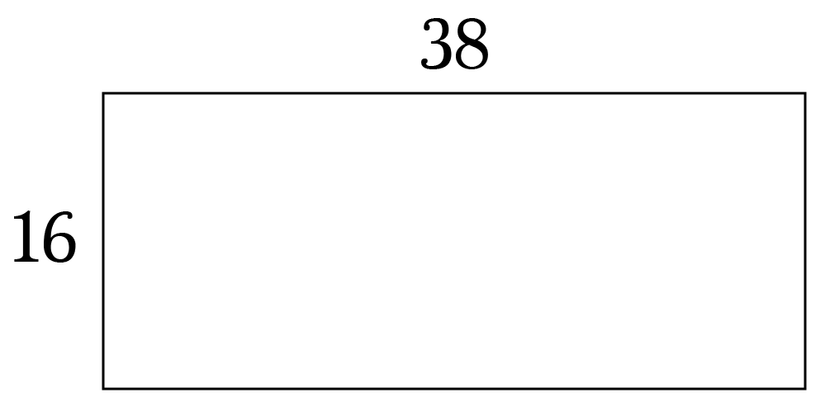
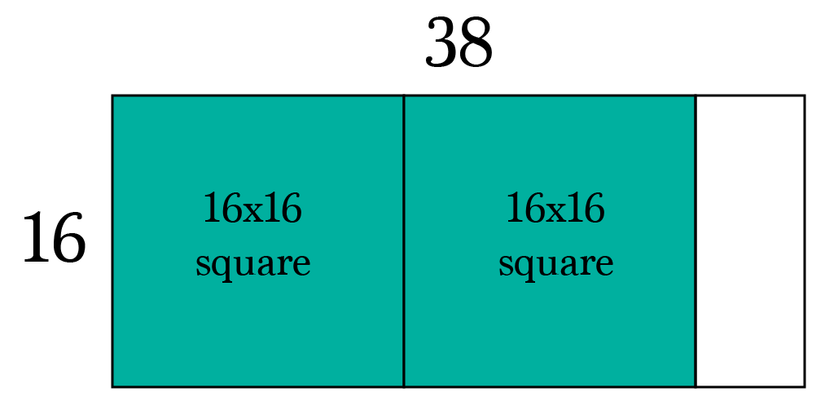
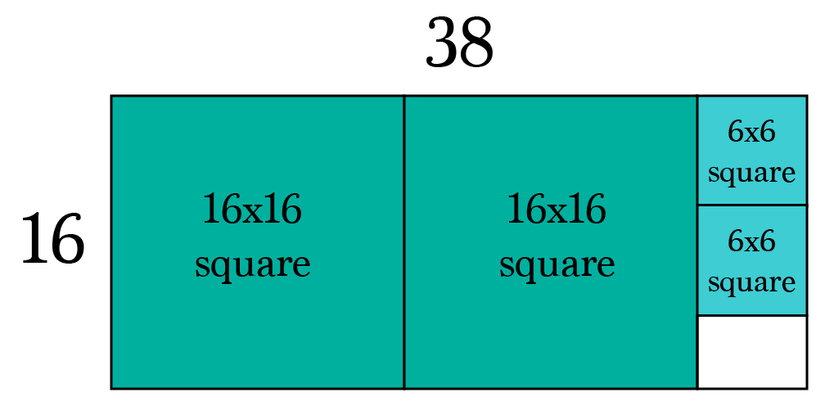
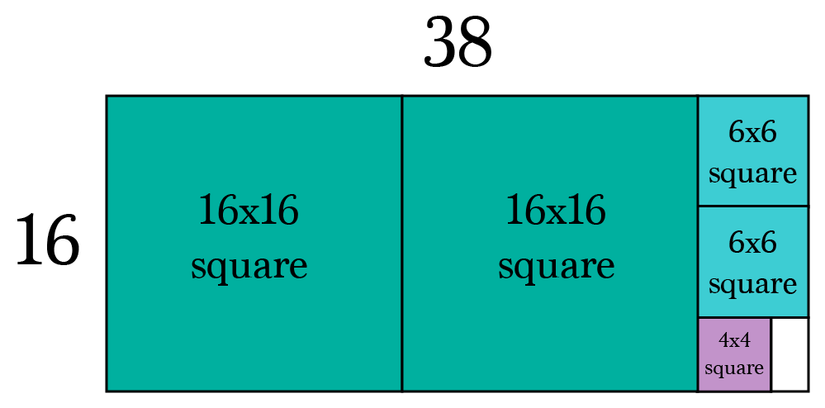
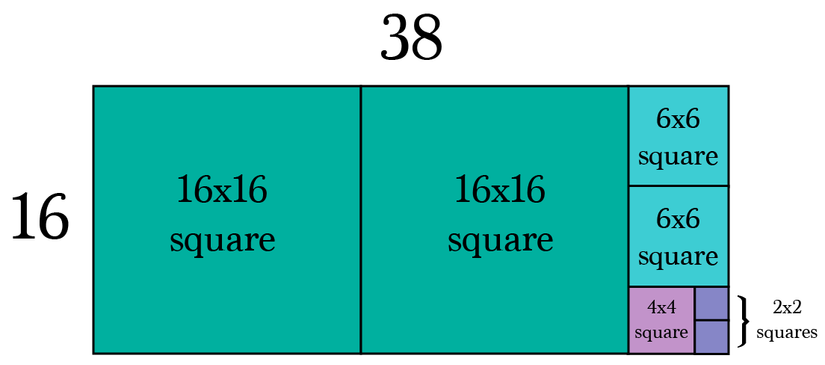
2. Proof of correctness
Nếu khảo sát thuật toán này, chúng ta có thể thấy rằng, thuật toán Euclidean sử dụng những tính chất sau:
- GCD(A,0) = A
- GCD(0,B) = B
- Nếu A = B⋅Q + R và B ≠ 0 thì GCD(A,B) = GCD(B,R) nếu Q là một số nguyên, R là một số nguyên ∈[0,B−1]in [0, B-1]
Hai tính chất đầu tiên cho phép chúng ta tìm ước chung lớn nhất nếu một trong hai số bằng 0, tính chất thứ ba cho phép chúng ta chuyển từ một vấn đề lớn hơn, khó giải quyết hơn thành một vấn đề nhỏ hơn, dễ giải quyết hơn.
Thuật toán Euclidean sử dụng tính chất thứ 3 để nhanh chóng chuyển bài toán ban đầu về một bài toán đơn giản hơn cho đến khi nó có thể được giải quyết bằng cách sử dụng một trong hai tính chất đầu tiên.
Và để hiểu hơn thì chúng ta sẽ bắt tay vào việc chứng minh những tính chất nêu trên là đúng.
GCD(A,0)=A
- Số nguyên lớn nhất A có thể chia hết chính là A
- 0 chia hết cho A
- 0 và A đều chia hết cho A nên GCD(A,0)=AGCD(A,0) = A
GCD(0,B)=B
- Tương tự như trên nhưng thay A bằng B.
GCD(A,B)=GCD(B,R)
Để chứng minh bổ đề trên, trước hết chúng ta cần chứng minh bổ đề sau đây là đúng: GCD(A,B)=GCD(B,A−B).GCD(A,B)=GCD(B,A-B).
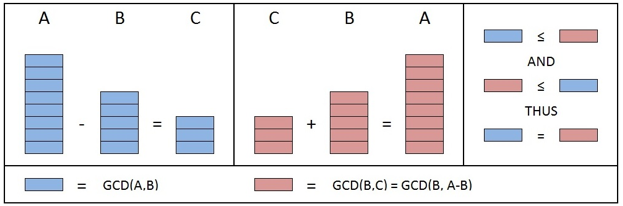
Giả sử chúng ta có ba số nguyên A, B và C sao cho A−B=CA-B = C
Ta có:
C=A−BA=X⋅GCD(A,B)B=Y⋅GCD(A,B)}⇒C=(X−Y)⋅GCD(A,B)begin{rcases}
C=A-B\
A=X⋅GCD(A,B) \
B=Y⋅GCD(A,B)
end{rcases}⇒C=(X – Y)⋅GCD(A,B)
=> C chia hết cho ước chung lớn nhất của A và B (1).
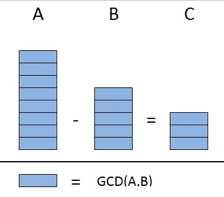
A=B+CB=M⋅GCD(B,C)C=N⋅GCD(B,C)}⇒A=(M+N)⋅GCD(B,C)begin{rcases}
A=B+C\
B=M⋅GCD(B,C) \
C=N⋅GCD(B,C)
end{rcases}⇒A=(M + N)⋅GCD(B,C)
=> A chia hết cho ước chung lớn nhất của B và C (2).
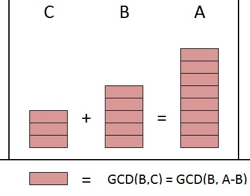
GCD(B,C) là ước chung lớn nhất của B và C (3).
GCD(A,B) là ước chung lớn nhất của A và B (4).
GCD(A,B)∣B,C (1)GCD(B,C)∣B,C (3)GCD(B,C)∣A,B (2)GCD(A,B)∣A,B (4)}⇒begin{rcases}
GCD(A,B) mid B, C& (1) \
GCD(B,C) mid B, C& (3)\
GCD(B,C) mid A,B& (2)\
GCD(A,B) mid A,B& (4)
end{rcases}⇒
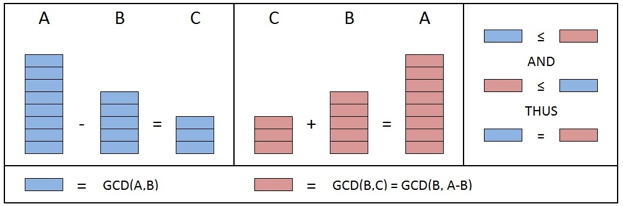
(1)(3) GCD(B,C)⩾GCD(A,B)(2)(4) GCD(A,B)⩾GCD(B,C)}⇒GCD(A,B)=GCD(B,C)⇒GCD(A,B)=GCD(B,A−B)begin{rcases}
(1)(3) & GCD(B,C) geqslant GCD(A,B) \
(2)(4) & GCD(A,B) geqslant GCD(B,C)
end{rcases}⇒GCD(A,B) = GCD(B,C)⇒GCD(A,B) = GCD(B,A-B)
A=B⋅Q+RGCD(A,B)=GCD(B,A−B)=GCD(A−B,B)}⇒begin{rcases}
A = B⋅Q + R\
GCD(A,B) = GCD(B,A-B) = GCD(A-B, B)\
end{rcases}⇒
A=B⋅Q+RGCD(A,B)=GCD(A−B,B)=GCD(A−2B,B)}⇒begin{rcases}
A = B⋅Q + R\
GCD(A,B) = GCD(A – B,B) = GCD(A – 2B,B)
end{rcases}⇒
R=A−B⋅QGCD(A,B)=GCD(A−B.Q,B)=GCD(R,B)}⇒GCD(A,B)=GCD(B,R)begin{rcases}
R = A – B⋅Q\
GCD(A,B) = GCD(A – B.Q,B) = GCD(R,B)
end{rcases}⇒ GCD(A,B) = GCD(B,R)
3. Reference
Nguồn: viblo.asia
