Tiếp theo chuỗi bài về Graph Convolution Network, hôm nay mình xin giới thiệu cho các bạn về mô hình GraphSage được đề cập trong bài báo Inductive Representation Learning on Large Graphs – một giải thụât inductive dùng cho đồ thị. Ủa inductive là gì thế ? Nếu bạn nào chưa rõ rõ khái niệm này thì chúng ta cùng tìm hiểu phần 1 nhé. Nếu bạn đã biết rôi thì chúng ta bỏ qua phần 1 để đến phần 2.

Dưới đây là một số thuật ngữ hoặc kí hiệu toán học mà mình sử dụng trong chuỗi bài này:

1. V: tập hợp các đỉnh của đồ thil
2. E: tập hợp các cạnh của đồ thị
3. D: ma trận đường chéo chứa thông tin bậc của mỗi đỉnh
4. A: ma trận vuông nhị phân (0 hoặc 1) chứa thông tin một nút có những hàng xóm hay nút kề nào
5. G: đồ thị được cấu thành.
6. N: số node của đồ thị
7. Xkvớik∈1,…,nX_{k} với k in {1, …, n}Xk​vớik∈1,…,n
8. I: ma trận identity với các phần tử trên đường chéo bằng 1 còn khác sẽ bằng 0
9. σ:haˋmsigmoidsigma: hàm sigmoidσ:haˋmsigmoid

I. Transductive learning và Inductive learning.

1. Transductive learning.

Transductive learning là quá trình học từ một tập dữ liệu huấn luyện cụ thể (training dataset) và dự đoán trên tập kiểm thử (test dataset) cụ thể. Ở đây nhãn cho cả hai tập huấn lụyện và kiểm thử đều đã được biết trước. Transductive learning được giới thiệu bởi Vladimir Vapnik
vào năm 1990. Ông có quan điểm rằng:

When solving a problem of interest, do not solve a more general problem as an intermediate step. Try to get the answer that you really need but not a more general one.

Dịch theo ý hiểu của mình là khi bạn giải quyết một vấn đề, đừng giải một vấn đề tổng quát hơn làm bằng trung gian. Thay vì đó, hãy cố gắng tìm câu trả lời mà bạn thực sự cần. Các giải thuật transductive learning có tính tổng quát hóa kém do đó khi có dữ liệu mới cần phải tiến hành huấn luyện lại.

2. Inductive learning

Inductive learning, ngược lại với transductive learning là quá trình học từ các tâp dữ liệu huấn luyện suy ra các quy luật chung rồi áp dụng các quy luât chung này vào tập kiểm thử. Với cách học này chúng ta không cần huấn luyện lại mạng khi có dữ liệu mới, chưa từng xuất hiện trong tập huấn luyện nên phù hợp giải cho các bài toán tổng quát hóa cao như bài toán về mạng xã hội, ….

II. Tìm hiểu mô hình GraphSgae.

Việc biểu diễn các đặc trưng đối tượng thành các đặc trưng của nút được nhúng trong đồ thị lớn đã được chứng minh hiệu quả trong nhiều các task dự đoán như gợi ý nội dung, …. Tuy nhiên các phương pháp transductive learning như kiến trúc GCN mình có trình bày tại Tản mạn về Graph Convolution Networks (Phần 1)
đều kém hiệu quả khi trong đồ thị xuất hiện các nút mới, chưa từng xuất hiện ở tập huấn luyện do GraphSage ra đời như một trong số lời giải cho vấn đề này. Chữ Sage trong GraphSage chính là viết tắt của hai từ Sample và Aggregate.

Ý tưởng chính GraphSage đó là thuật toán tạo ra các embedding vector cho nút mới chưa được huấn luyện được gọi là embedding generation algorithm. Giải thuật thực hiện bằng cách huấn luyện một tập hợp các hàm gọi là aggregator function giúp tổng hợp các thông tin đặc trưng từ các nút hàng xóm. Mỗi aggregator function tổng hợp đặc trưng nhiều thông tin khác ở mỗi nút.

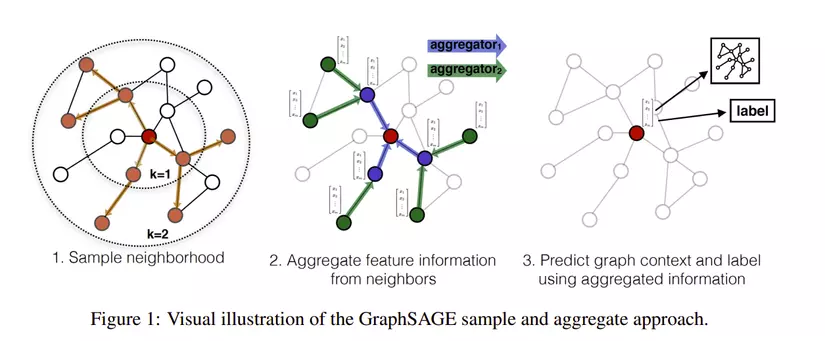
Để tìm hiểu chi tiết về ý tưởng này, mình sẽ trình bày 3 phần dựa trên bài báo nghiên cứu của tác giả đó là:

• Giải thuật sinh ma trận embedding cho từng nút
• Hàm mất mát
• Các kiến trúc hàm tổng hợp phổ biến.

1. Giải thuật sinh ma trận embedding

Trước khi đi chi tiết phần giải thuật có một số ký hiệu được tác giả quy ước:

• K: Search depth, số lớp của mô hình
• AGGREGATEk,∀k∈{1,…,K}AGGREGATE_{k}, forall k in {1, …, K}AGGREGATEk​,∀k∈{1,…,K}: K hàm aggregator
• Wk,∀k∈{1,…,K}W^{k}, forall k in {1, …,K}Wk,∀k∈{1,…,K}: ma trận trọng số dùng cho mỗi lớp của mô hình
• NvN_{v}Nv​: tập hợp các nút hàng xóm của nút v
• xv,∀v∈Vx_{v}, forall v in Vxv​,∀v∈V: feature của toàn bộ các nút

Ở mỗi vòng lặp k, giải thuật được thực hiện như sau:

• Với mỗi nút $v\in V$,
  1. Đặc trưng của các nút hàng xóm của nút v tại bước k – hN(v)kh_{N(v)}^khN(v)k​ bằng output của hàm aggregator với input là đặc trưng nút đó ở step k – 1
  2. Thực hiện concat đặc trưng nút v ở bước k -1 hvk−1h_{v}^{k – 1}hvk−1​ với hN(v)kh_{N(v)}^khN(v)k​ và cho ma trận sau khi qua concat vào một lớp fully connected với một hàm nonlinear activation $\sigma$.
  3. Kết quả vừa tính ở bước 2 sẽ tiếp tục được dùng ở các vòng lặp tiếp theo.
• Đặc trưng của mỗi nút v ở bước k được normalize bằng cách chia cho norm 2 của chính nó

Cuối cùng sau khi thực K vòng lặp, đặc trưng cuối cùng của mỗi nút v được kí hiệu là zvz_{v}zv​.

Có 1 điểm khác biệt giữa định nghĩa hàng xóm ở giải thuật GraphSage và định nghĩa hàng xóm ở bài báo SEMI-SUPERVISED CLASSIFICATION WITH
GRAPH CONVOLUTIONAL NETWORKS đó là ở giải thuật GraphSage chúng ta chỉ lấy ngẫu nhiên tập hàng xóm có kích thước cố định chứ không phải lấy toàn bộ hàng xóm. Điều này sẽ giảm kích thước giúp mô hình tính toán nhanh hơn đặc biệt trong những bài toán có đồ thị lớn.

2. Hàm mất mát của giải thuật GraphSage.

Các hàm mất mát dựa trên cơ chế khuyến khích các nút gần nhau sẽ có biểu diễn tương tự nhau trong khi các nút khác nhau sẽ có biểu diễn khác nhau.

JG(zu)=−log⁡(σ(zuτ‾zv))−Q⋅Evn∼Pn(v)log⁡(σ(−zuτ~‾zvn)),J_{cal G}({bf z}_{u})=-logleft(sigma({bf z}_{u}^{overline{{bftau}}}{bf z}_{v})right)-Qcdot{bf E}_{v_{n}sim P_{n}(v)}logleft(sigma(-{bf z}_{u}^{overline{tilde{bftau}}}{bf z}_{v_{n}})right),
JG​(zu​)=−log(σ(zuτ​zv​))−Q⋅Evn​∼Pn​(v)​log(σ(−zuτ~​zvn​​)),

trong đó:

• v là một nút gần u được lấy ngẫu nhiên theo random walk có chiều dài cố định.
• PnP_{n}Pn​: negative sampling distribution
• Q: số lượng negative samples hay các nút không kề nhau.

Ta có thể thấy với việc sử dụng hai nút không kề nhau một cách ngẫu nhiên đã khiến cho mô hình có tính tổng quát cao hơn đối đặc biệt khi dự đoán vào các dữ liệu chưa được huấn luyện.

3. Các kiến trúc hàm tổng hợp phổ biến.

Không giống với các dạng dữ liệu như câu văn, ảnh, … , các nút hàng xóm không có thứ tự do đó các hàm tổng hợp phải có tính đối xứng tức là bất biến đối với sự thay đổi thứ tự trong input đầu vào trong khi vẫn có thể huấn luyện và có khả năng biếu diễn, trích xuất đặc trưng cao. Theo bài báo, tác giả có đề cập đến các loại hàm tổng hợp như sau:

3.1. Mean aggregator

Hàm mean aggregator có nghĩa là trung bình theo elementwise các vector huk−1,∀u∈N(v)h_{u}^{k – 1}, forall u in N(v)huk−1​,∀u∈N(v). Khi sử dụng mean aggregator, câu lệnh dòng 4, 5 ảnh 1 trong thuật toán sinh embedding được viết như sau:

hvk←σ(W⋅MEAN({hvk−1}∪{huk−1,∀u∈N(v)}).mathbf { h } _ { v } ^ { k } leftarrow sigma ( mathbf { W } cdot mathbf { M E A N } ( { mathbf { h } _ { v } ^ { k – 1 } } cup { mathbf { h } _ { u } ^ { k – 1 } , forall u in { cal { N } } ( v ) } ) .
hvk​←σ(W⋅MEAN({hvk−1​}∪{huk−1​,∀u∈N(v)}).

Việc thực hiện concat được miêu tả như dòng trên giống như một skip-connection giữa các layer khác nhau trong thuât toán GraphSage và theo tác giả đây chính là yếu tố giúp hiệu suất thuật toán được cải thiện.

3.2. LSTM aggregator

Trong bài báo, tác giả cũng có đề câp sử dụng LSTM làm aggregator. Chúng ta thường thấy LSTM thường xuất hiện trong các bài toán xử lý dữ liệu tuần tự như text, …. Tuy nhiên các nút trong đồ thị không có thứ tự nào cả do đó chúng ta cần xáo trộn ngẫu nhiên các nút hàng xóm khi cho dữ liệu đi qua LSTM để đảm bảo tính tổng quát của mô hình.

3.3. Pooling aggregator.

Pooling aggregator sau đây là hàm đối xứng và có thể huấn luyện. Mỗi vecot của nút hàng xóm sẽ được truyền một cách độc lập qua một lớp fully connected và sau đó chúng ta thực max-pooling để tổng hợp thông tin từng phần tử tương ứng trên các nút hàng xóm được chọn.

AGGREGATEkpod= max({σ(Wpoolhuik+b),∀ui∈N(v)}),mathrm{AGGREGATE_{k}^{mathrm{pod}}= m a x({sigmaleft({bf W}_{mathrm{pool}}{bf h}_{u_{i}}^{k}+{bf b}right),forall u_{i}in{cal N}(v)}),}
AGGREGATEkpod​= max({σ(Wpool​hui​k​+b),∀ui​∈N(v)}),

Ý tưởng lớp pooling này ta thấy tương tự như việc sắp xếp các lớp trong neural network truyền thống: FC -> Pooling. Nhờ vậy mô hình có thể biễu diễn đặc trưng của các nút hàng xóm tốt hơn.

III. Lời kết

Ở bài viết này mình đã trình bày qua về giải thuật GraphSage. Giải thuạt này có ưu điểm so với mô hình GCN mình đã trình bày ở bài trước ở một số điểm như tính tổng quát hóa cao hơn với dữ liệu chưa được huấn luyện nhờ vào các aggregator function và có một số cải thiện tốc độ tính toán thông qua việc giảm kích thước ma trận các nút hàng xóm trong quá trình tính toán ma trận embedding của một nút. Tuy nhiên vấn đề huấn luyện hoặc inference theo các sub-graph ở mô hình GCN trong bài trước vẫn chưa được cải thiện. Lời giải cho vấn đề này sẽ được mình giới thiệu cho bài viết tiếp theo. Cảm ơn các bạn đã đọc và theo dõi bài viết của mình.

Tài liệu tham khảo

1. [Deep Learning] Graph Neural Network – A literature review and applications
2. Inductive Representation Learning on Large Graphs