I. Lời mở đầu

Chắc hẳn, ai trong số chúng ta khi bắt đầu học Tin học đều nghe qua khái niệm: Cấu trúc dữ liệu (Data Structures) và Giải thuật (Algorithm). Không sai, đây chính là hai chủ đề lớn và vô cùng quan trọng trong Lập trình thi đấu nói riêng và trong Công nghệ thông tin nói chung. Nhà khoa học máy tính Niklaus Wirth đã từng nói một câu rất nổi tiếng: Chương trình = Cấu trúc dữ liệu + Giải thuật (Program = Data Structures + Algorithms). Trong chủ đề này, chúng ta sẽ cùng bàn về một số chiến lược thiết kế giải thuật phổ biến và ứng dụng của chúng

Có rất nhiều các chiến lược thiết kế giải thuật khác nhau trong thế giới thuật toán, chúng được phát triển qua các thời kỳ của nhân loại và ngày càng tăng cao về hiệu năng. Mỗi giải thuật đều có vị thế nhất định của chúng, nhưng chỉ là những giải thuật tổng quát và áp dụng cho một số lớp bài toán nhất định, chứ không thể tồn tại một phương pháp vạn năng để giải quyết mọi bài toán. Chủ đề này, mình sẽ giới thiệu tới các bạn một số thiết kế giải thuật, bao gồm: Quay lui, Nhánh và cận, Tham lam, Chia để trị và Quy hoạch động. Những phương pháp này sẽ được trình bày một cách định hướng, kèm theo một số ví dụ cụ thể để bạn đọc hiểu được cách xây dựng thuật toán từ những chiến lược tổng quát.

II. Phương pháp quay lui

1. Phát biểu bài toán

Quay lui, duyệt vét cạn, thử sai,…là một số những tên gọi mà các bạn có thể thường nghe về phương pháp quay lui, nhưng tất cả chúng đều có chung một ý nghĩa trong Tin học: Tìm nghiệm của bài toán bằng cách xem xét tất cả các phương án có thể. Đối với máy tính, nhờ vào tốc độ tính toán nhanh và khả năng lưu trữ lớn, máy tính có thể giải quyết rất nhiều bài toán bằng cách thử mọi khả năng – việc mà đối với con người gần như là bất khả thi. Thuật ngữ “quay lui” lần đầu tiên được đề xuất vào những năm 1950 bởi nhà Toán học người Mỹ Derrick Henry Lehmer.

Trong nhiều bài toán, việc tìm nghiệm có thể quy về việc tìm một tập hữu hạn các thành phần ${x_1, x_2,…, x_n,…}$ với độ dài của tập có thể xác định trước hoặc không. Mỗi thành phần $x_i$ sẽ được lựa chọn từ một tập hợp $A_i$ hữu hạn. Ngoài ra, tập này cũng cần thỏa mãn một số điều kiện của bài toán đề ra.

Nói như vậy có thể hơi khó hiểu, dưới đây mình xin trích ví dụ Bài toán 8 quân hậu từ Sách giáo khoa chuyên Tin quyển I của thầy Hồ Sĩ Đàm để làm rõ tư tưởng của phương pháp:

Một bàn cờ vua $8 \times 8$ đang để trống. Cần đặt $8$ quân hậu khác nhau vào bàn cờ vua sao cho không có hai quân hậu nào tấn công được nhau, biết rằng hai quân hậu sẽ tấn công nhau nếu như chúng đứng cùng hàng, cùng cột hoặc cùng đường chéo.

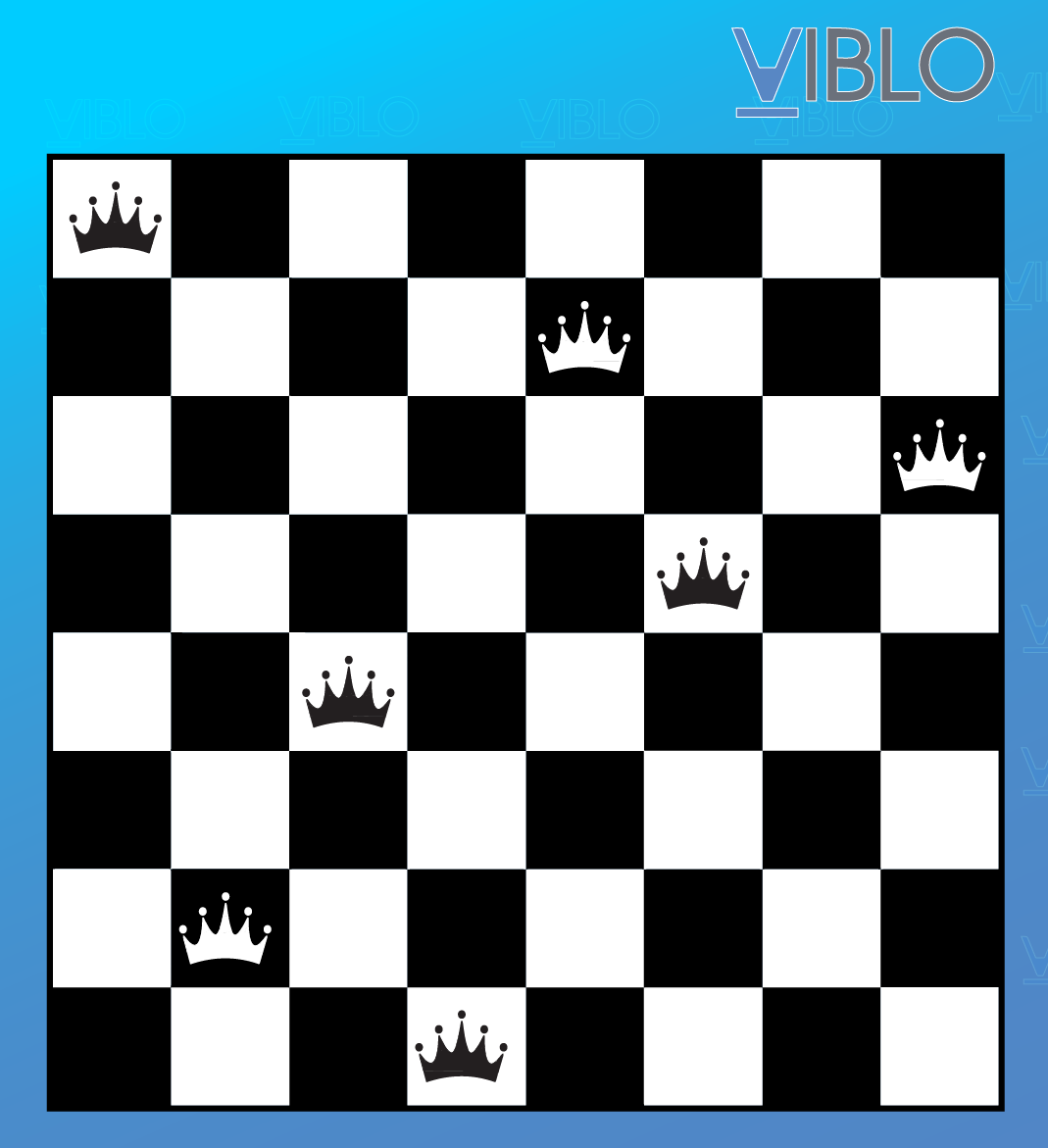
Một cách đặt hậu thỏa mãn yêu cầu

Ta nhận thấy, các quân hậu cần được đặt trên các hàng khác nhau. Nếu đánh số các quân hậu từ $1$ tới $8,$ thì quân hậu thứ $i$ sẽ nằm trên hàng ngang thứ $i$ . Gọi $x_i$ là cột mà quân hậu thứ $i$ nên đặt vào, thì nghiệm của bài toán sẽ quy về tìm tập ${x_1, x_2,…, x_8},$ trong đó $x_i le 8,$ nghĩa là $x_i$ chọn từ tập $A_i = {1, 2,…, 8}$ . Điều kiện để tập ${x_1, x_2,…, x_8}$ là một nghiệm của bài toán là $xi≠xjx_i ne x_j$ và hai ô $i, x_i), (j, x_j)$ không nằm trên cùng một đường chéo.

2. Tư tưởng phương pháp

Ý tưởng của phương pháp quay lui dựa trên việc thử tất cả các trường hợp của nghiệm, cụ thể như sau:

Giả sử ta cần xây dựng tập nghiệm ${x_1, x_2,…, x_n},$ thì ta sẽ đi xây dựng từng thành phần một, bắt đầu từ tập rỗng. Thành phần $x_1$ sẽ được chọn ra từ tập $S_1 = A_1$ . Giả sử bạn đã xây dựng được ccác thành phần $x_1, x_2,…, x_{i – 1},$ thì từ các điều kiện của bài toán, chúng ta có thể xác định được tập các $S_i$ là ứng cử viên cho thành phần $x_i$ ( $S_i$ là tập con của $A_i$ ). Từ tập $S_i,$ chỉ cần chọn ra một ứng cử viên cho $x_i$ thì ta sẽ mở rộng được nghiệm thành $x_1, x_2,…, x_{i – 1}, x_i$ . Tiếp tục lặp lại quá trình trên để mở rộng nghiệm.
Nếu như khi xây dựng tới $x_{i + 1}$ mà không thể chọn được ứng cử viên nào cho nó (tập $S_i$ rỗng), thì ta quay lại chọn một phần tử khác của $S_i$ cho $x_i$ . Nếu tập $S_i$ cũng không còn phần tử nào khác, thì lại quay lại chọn một phần tử khác trong tập $S_{i – 1}$ cho $x_{i – 1},…$và cứ thế tiếp tục. Trong quá trình mở rộng nghiệm, ta cần kiểm tra xem nghiệm đang xây dựng đã phải là nghiệm của bài toán hay chưa. Nếu chỉ cần tìm một nghiệm thì khi gặp nghiệm ta dừng lại, còn nếu cần tìm tất cả các nghiệm thì cần phải quét qua mọi khả năng lựa chọn các thành phần của vector nghiệm.

Lược đồ tổng quát của phương pháp thường được thể hiện bằng mô hình đệ quy như sau:

// Xây dựng thành phần thứ i của vector nghiệm.voidbacktracking(i){{Xác_định_tập_S[i]};for(value in S[i]){{Ghi_nhận_thành_phần_x[i]= value};if{tìm_thấy_nghiệm}:{{Đưa_ra_nghiệm};}else{// Gọi đệ quy để xây dựng thành phần thứ i + 1.backtracking(i +1);}// Còn gọi là "trả đệ quy", xóa thành phần thứ i đi để chọn giá trị khác cho nó. {Loại_bỏ_thành_phần_thứ_i};}}

Như vậy, khi áp dụng lược đồ tổng quát của phương pháp Quay lui cho các bài toán cụ thể, có ba vấn đề quan trọng mà các bạn cần lưu tâm:

Tìm cách biểu diễn nghiệm của bài toán dưới dạng một dãy các đối tượng chọn dần từng bước: ${x_1, x_2,…, x_i,…}$ .
Xác định tập $S_i$ là các ứng cử viên có thể lựa chọn cho thành phần $x_i$ và tìm cách biểu diễn phù hợp.
Tìm ra các điều kiện để một tập các thành phần đã chọn trở thành nghiệm của bài toán.

Như vậy mình đã giới thiệu tới các bạn toàn bộ lí thuyết tổng quan về phương pháp quay lui. Tất nhiên, từ lí thuyết tới thực tế cách xa nhau rất nhiều, vì thế, các bạn hãy cùng chuyển sang phần $2$ của bài viết này để cùng mình phân tích một số bài toán ví dụ áp dụng phương pháp quay lui nhé!

Nguồn: viblo.asia

Quay lui (Backtracking) (Phần 1)

I. Lời mở đầu

II. Phương pháp quay lui

1. Phát biểu bài toán

2. Tư tưởng phương pháp

Bài viết liên quan

WebP là gì? Hướng dẫn cách để chuyển hình ảnh jpg, png qua webp

Điểm khác biệt giữa IPv4 và IPv6 là gì?

Check nameservers của tên miền xem website trỏ đúng chưa

Mình đang dùng Google Domains để check tên miền hàng ngày

Liên hệ

THÔNG TIN

Địa chỉ