[Paper Explained] TimeSformer: Are Transformers the Game-changer for Action Recognition?

Gần đầy, các bài toán trong lĩnh vực NLP thường sử dụng một phương pháp “không cũ không mới” mang tên self-attention. Lý do chính là vì phương pháp này có thể giữ được các thông tin của ngữ cảnh (mặc dù độ dài của sequence đầu vào có thể rất lớn) mà vẫn cho phép tính toán song song (parallelization) – điểm mạnh của việc sử dụng GPU. Điển hình, ta có ví dụ về kiến trúc mạng Transformers, một kiến trúc đã làm thay đổi toàn bộ hướng tiếp cận về các bài toán xử lý ngôn ngữ tự nhiên trong thời gian vài năm đổ lại. Vấn đề được đặt ra trong bài viết này là, liệu ta có thể sử dụng lợi thế đó vào các bài toán trong lĩnh vực CV, như là bài toán Action Recognition?

Hình 1. Transformers Revolution – Cuộc khởi nghĩa của kiến trúc Transformers

1. Đặt vấn đề cho bài toán Action Recognition:

1.1 Tại sao lại là Transformers?

Action Recognition là bài toán về việc nhận biết và phân loại hành động có trong video. Như chúng ta đã biết, video là một chuỗi các frame ảnh liên tiếp, có liên quan tới nhau. Một video thường sẽ chứa 2 chiều là Không gian (Spatial) – nội dung của từng frame trong video và Thời gian (Temporal) – sự liên kết của các frame trong video. Các bạn thấy quen không ? Nó chính là dạng dữ liệu sequence, giống với một câu văn: 1 frame ảnh ứng với 1 từ trong câu, vị trí của từ trong câu tương ứng với vị trí của frame trong video. Vậy là ta có thể hoàn toàn áp dụng Transformers vào video như dạng sequence data bình thường. Nhưng tại sao lại là Transformers, tại sao không dùng CNN? Ta có thể kể đến một số lý do như sau:

• Transformers – Self-attention có thể nắm bắt được vị trí của các thành phần trong sequence nhờ vào positional embedding.
• CNN bị mất quá nhiều thông tin, chủ yếu là do các lớp pooling để làm giảm computational cost.
• Không có inductive biases, dẫn tới kết quả được chính xác hơn nhiều mà không bị vấn đề overfitting.
• Trong bài toán Video Classification, các phương pháp từ trước tới nay hay sử dụng nền tảng là lớp 3D-CNN (do lớp CNN truyền thống chỉ có khả năng nắm bắt thông tin trong 1 khoảng không-thời gian nhỏ) và chi phí tính toán mà các cách trên yêu cầu là cực kỳ cao, cả về năng lực xử lý lẫn thời gian Training-Inference. Ngoài ra, các mạng sử dụng thuần kiến trúc 3D-CNN cũng không thể áp dụng cho các video có độ dài quá lớn.

Hình 2. Lợi thế của kiến trúc Transformers

1.2 Nhược điểm và cách khắc phục:

Okay, lợi thế rõ ràng. Transformers, tớ chọn cậu! Nhưng để cậu này áp dụng được vào bài toán Action Recognition thì lại là một vấn đề khác. Giả sử, nếu chúng ta cứ lấy video có độ phân giải là 256×256 thì với mỗi frame, số lượng pixel trong 1 frame sẽ là $256\ast 256=62500$. Khi áp dụng self-attention, mỗi một phần tử sẽ cần phải tính toán trên tất cả các phần tử còn lại, hay nói cách khác là O(n2)O(n^2)O(n2), khi đó số lượng phép tính sẽ là 625002=390625000062500^2=3906250000625002=3906250000. Hơn 3 tỷ phép tính cho 1 frame có độ phân giải 256×256. Nếu giả sử video đó dài 10 giây, mỗi giây có 30 frame (30fps) thì cúng ta sẽ cần tính (256∗256∗30∗10)2=386547056640000(256*256*30*10)^2= 386547056640000(256∗256∗30∗10)2=386547056640000. Gần 400 nghìn tỷ phép tính cho một video ngắn 10s và độ phân giải gần bằng 240p, nghe có vẻ vừa lâu vừa lãng phí nhỉ?

Hình 3. Self-attention từng pixel trong một bức ảnh sẽ nhiều đến như nào?

Vì vậy, TimeSformer đã áp dụng 2 cách thức nhằm giải quyết vấn đề trên của Transformers:

• Chia frame thành các patches, mỗi patches sẽ đại diện cho một phần tử để tính toán self-attention. Đây là phương pháp đã được áp dụng trong mạng ViT (Vision Transformers) nhằm giảm số lượng phần tử cần tính trong self-attention mà vẫn giữ được đầy đủ thông tin cần thiết. Trong bài, tác giả đã đặt kích thước của từng patch là 16×16, trùng với kích thước patch có trong paper gốc của ViT. Về chi tiết cách vận hành, mình sẽ nói chi tiết hơn ở phần sau.
• Sử dụng cơ chế Space-Time divided the Attention. Trong chiều thời gian, từng patch chỉ tập trung vào các patches có cùng vị trí trong các frame còn lại. Mặt khác, trong chiều không gian, từng patch chỉ tập trung vào các patches khác trong cùng frame. Có tổng cộng 5 cơ chế lấy neighbors cho phép attention trong paper, chi tiết từng cách cũng sẽ được mình nói chi tiết hơn ở phần 2.

Hình 4. Patches of pixel trong ảnh

2. TimeSformer: Is Space-Time Attention All You Need for Video Understanding?

Mình sẽ trình bày theo trình tự từ Input – Process&Output như paper. Mỗi phần mình sẽ tóm tắt và giải thích, tuy nhiên các kiến thức chuyên sâu tới self-attention và Transformers mình sẽ không nhắc lại, các bạn có thể tham khảo ở các bài như Tản mạn về Self Attention và Transformers – “Người máy biến hình” biến đổi thế giới NLP để hiểu sâu hơn nếu chưa tìm hiểu nhé.

2.1 Input:

Đầu vào của mạng là một clip ngắn được cắt ra từ video gốc. Video sẽ có kích thước (H, W, 3, F) cùng với một vài thông số: N, P và F/Fs; Ngoài ra, mặc định các video sẽ đều có mức Frame Per Second là 30. Chi tiết hơn về những thông số trên như sau:

• (H,W) chính là độ phân giải của video, sẽ được resize sao cho H và W có cùng kích thước (frame sẽ có dạng hình vuông).
• 3 là số channel màu (RGB).
• F là số frame của video ngắn đó.
• P là kích thước của patch, mặc định trong paper là 16×16 pixel.
• N là số patches có trong 1 frame, công thức H∗WP2frac{H*W}{P^2}P2H∗W​.
• F/Fs là số lượng các frame liên tiếp trong video gốc để chọn lọc ra 1 frame. Ví dụ: Ta có 128 frames, F/Fs là 1/32 thì sẽ có tổng cộng 4 frame được chọn thành clip.

Từ các thông số trên, tác giả đã đưa ra 3 mạng với các thiết lập khác nhau, với các tên gọi như TimeSformer – baseline, TimeSformer-HR – video có độ phân giải cao (High Resolution) và TimeSformer-L – video dài (Long) như sau:

• TimeSformer: 224 × 224 × 3 × 8, F/Fs: 1/32.
• TimeSformer-HR: 448 × 448 × 3 × 8, F/Fs: N/A.
• TimeSformer-L: 224 × 224 × 3 × 96, F/Fs: 1/4.

Dễ dàng thấy, với các thông số trên, thời gian clip đầu vào của mạng đầu tiên sẽ là $8/(1/32)/30=8.5s$, mạng L sẽ là $96/(1/4)/30=12.8s$. Đối với các tập dữ liệu để benchmark cho bài Action Recognition như Kinetic hay SSv2, thời gian 1 clip chỉ rơi vào khoảng 10s thì ba mạng trên là rất phù hợp. Tuy nhiên, đối với video thực tế, thời lượng trên là quá ngắn. Vì vậy, giải pháp của authors là chia video gốc thành các video ngắn hơn với length của các clip đó sẽ có giá trị giống với đầu vào của mạng, sau đó sẽ tính toán kết quả của từng clip được cắt và tính trung bình để ra kết quả cuối cùng.

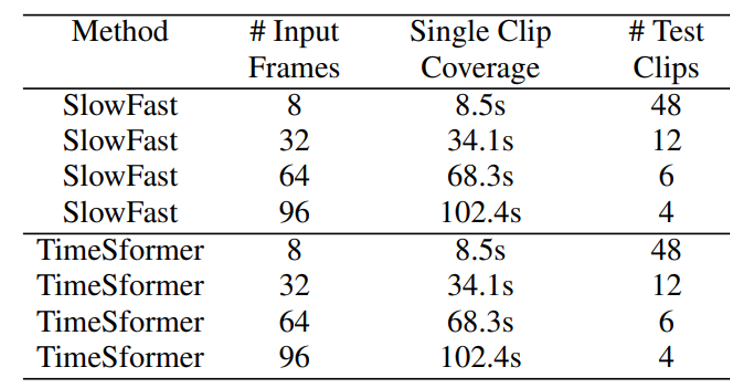
Hình 5. Mạng TimeSformer đã được tinh chỉnh và thống kê trên tập HowTo100M

Video sau khi được cắt thành các clips sẽ được chia thành các patch. Khi cắt xong, ta sẽ flatten thành 1 vector chứa 2 nội dung: Vị trí của patch đó trong frame và vị trí của frame chứa patch đó trong clips để tiến hành truyền vào mạng process. Đây chính là phần positional embedding của đầu vào mạng Transformers truyền thống, ta đặt tên là e(p,t)posmathbf{e}_{(p, t)}^{p o s}e(p,t)pos​.

2.2 Process&Output:

Bước này đơn thuần sẽ xử lý theo luồng cấu trúc Transformers bình thường, tuy nhiên ta sẽ không có phần decoder do ta chỉ cần sinh embedding và tiến hành classify. Tóm tắt quá trình process như sau:

• Tạo embedding context của từng patch, sau đó kết hợp nhân với một ma trận weight có thể học được và cộng position embedding đã tạo ở bước trước để ra word (mình cũng không biết đặt tên như nào nên sẽ mượn tạm tên gọi của Transformers NLP). Công thức như sau:

z(p,t)(0)=Ex(p,t)+e(p,t)posmathbf{z}_{(p, t)}^{(0)}=E mathbf{x}_{(p, t)}+mathbf{e}_{(p, t)}^{p o s}
z(p,t)(0)​=Ex(p,t)​+e(p,t)pos​

        với $E$ là ma trận học được và x(p,t)mathbf{x}_{(p, t)}x(p,t)​ là embedding context.

• Tính toán 3 giá trị của Query-Key-Value dựa vào WQ-WK-WV giống như cơ chế Transformers. Công thức để tính toán ra 3 giá trị trên:

q(p,t)(ℓ,a)=WQ(ℓ,a)LN⁡(z(p,t)(ℓ−1))∈RDhk(p,t)(ℓ,a)=WK(ℓ,a)LN(z(p,t)(ℓ−1))∈RDhv(p,t)(ℓ,a)=WV(ℓ,a)LN⁡(z(p,t)(ℓ−1))∈RDhbegin{aligned}
&mathbf{q}_{(p, t)}^{(ell, a)}=W_{Q}^{(ell, a)} operatorname{LN}left(mathbf{z}_{(p, t)}^{(ell-1)}right) in mathbb{R}^{D_{h}}\
&mathbf{k}_{(p, t)}^{(ell, a)}=W_{K}^{(ell, a)} mathrm{LN}left(mathbf{z}_{(p, t)}^{(ell-1)}right) in mathbb{R}^{D_{h}}\
&mathbf{v}_{(p, t)}^{(ell, a)}=W_{V}^{(ell, a)} operatorname{LN}left(mathbf{z}_{(p, t)}^{(ell-1)}right) in mathbb{R}^{D_{h}}
end{aligned}
​q(p,t)(ℓ,a)​=WQ(ℓ,a)​LN(z(p,t)(ℓ−1)​)∈RDh​k(p,t)(ℓ,a)​=WK(ℓ,a)​LN(z(p,t)(ℓ−1)​)∈RDh​v(p,t)(ℓ,a)​=WV(ℓ,a)​LN(z(p,t)(ℓ−1)​)∈RDh​​

        với $l$ là patch đang được xét và $LN()$ là hàm LayerNorm.

• Tính toán multi-head self-attention dựa theo công thức mul dot-product ở cả 2 chiều Spatial và Temporal. Tuy nhiên, ở bước này, sẽ có vài cách tính self-attention khác nhau (mình sẽ nói ở phần dưới). (1)
• Tạo encoding từ các kết quả của bước trên, kết hợp với kết nối tắt residual connection và đưa qua một lớp MLP để feed kết quả cho lớp tiếp theo. Với … là kết quả từ phép dot-product ở trên, ta sẽ có công thức như sau:

z(p,t)′(ℓ)=WO[s(p,t)(ℓ,1)⋮s(p,t)(ℓ,A)]+z(p,t)(ℓ−1)z(p,t)(ℓ)=MLP⁡(LN⁡(z(p,t)′(ℓ)))+z(p,t)(ℓ)begin{gathered}
mathbf{z}_{(p, t)}^{prime(ell)}=W_{O}left[begin{array}{c}
mathbf{s}_{(p, t)}^{(ell, 1)} \
vdots \
mathbf{s}_{(p, t)}^{(ell, mathcal{A})}
end{array}right]+mathbf{z}_{(p, t)}^{(ell-1)} \
mathbf{z}_{(p, t)}^{(ell)}=operatorname{MLP}left(operatorname{LN}left(mathbf{z}_{(p, t)}^{prime(ell)}right)right)+mathbf{z}_{(p, t)}^{(ell)}
end{gathered}
z(p,t)′(ℓ)​=WO​⎣⎢⎢⎢⎡​s(p,t)(ℓ,1)​⋮s(p,t)(ℓ,A)​​⎦⎥⎥⎥⎤​+z(p,t)(ℓ−1)​z(p,t)(ℓ)​=MLP(LN(z(p,t)′(ℓ)​))+z(p,t)(ℓ)​​

        z(p,t)(ℓ)mathbf{z}_{(p, t)}^{(ell)}z(p,t)(ℓ)​ chính là giá trị đầu ra của một khối trên, đây cũng sẽ là giá trị đầu vào của khối self-attention tiếp theo.

• Embedding cuối cùng sẽ được đưa qua một lớp MLP cuối, dùng để classify về n-classes tùy vào bài toán.

y=LN⁡(z(0,0)(L))∈RDmathbf{y}=operatorname{LN}left(mathbf{z}_{(0,0)}^{(L)}right) in mathbb{R}^{D}
y=LN(z(0,0)(L)​)∈RD

Kết quả cuối cũng sẽ là một vector xác suất ứng với số lượng các class có trong bài toán ($y$). Vậy là chúng ta đã xong flow của model, tuy nhiên, mình vẫn chưa trình bày về cơ chế self-attention của authors, một cơ chế mới thay cho cơ chế self-attention truyền thống, mang tên Divided Space-Time Attention .

2.3 Divided Space-Time Attention:

Do chúng ta cần tính self-attention không chỉ trên các patches trong 1 frame, mà còn tất cả các frames trong 1 clip. Vì vậy, ta phải cải thiện cách lấy neighbors (những patch sẽ được tính trong phép tính của self-attention), sao cho đảm bảo việc thể hiện được sự tương quan giữa các patch trong 1 khung hình, mà còn cả sự liền mạch của thời gian giữa các frame. Authors của paper đã giới thiệu 5 cách lấy sau:

Hình 6. Năm phương pháp lấy neighbors self-attention khác nhau

Lưu ý rằng, mỗi một ô vuông nhỏ là 1 patch, màu xanh dương đại diện cho patch được xét, màu đỏ đại diện cho neighbors được xét theo chiều Spatial (không gian), màu xanh lá cây đại diện cho neighbors được xét theo chiều Temporal (thời gian), màu vàng đại diện cho neighbors được xét trong khoảng local, màu tím đại diện cho neighbors được xét trong khoảng global. Mình sẽ tóm tắt cách lấy của từng phương pháp như sau:

• Space Attention (S): Chỉ thực hiện trên tất cả các image patches ở cùng 1 frame, không quan tâm tới các frame khác.
• Joint Space-Time Attention (ST): Thực hiện trên tất cả các image patch ở tất cả các frame.
• Divided Space-Time Attention (T+S): Trước tiên, thực hiện tính toán trên tất cả image patch trong 1 frame (chiều Spatial), sau đó thực hiện trên các patch của các frames khác trước và sau đó mà có cùng vị trí với patch đang xét trong frame (chiều Temporal).
• Sparse Local Global Attention (L+G): Đầu tiên thực hiện việc self-attention locally bằng cách thực hiện trên các patch ở liền kề, sao cho kích thước bao quát của local neighbor sẽ bằng H/2 × W/2 và trải dài tất cả các frame. Sau đó, ta sẽ tính toán tới phần globally bằng cách sử dụng các stride = 2 ở cả 2 chiều là W và H, xuyên suốt toàn bộ frames.
• Axial Attention (T+W+H): Giống với cơ chế Divided Space-Time Attention, tuy nhiên giảm bớt ở chiều Spatial còn là cột (trở thành chiều Global) và hàng (trở thành chiều Local) ứng với điểm đang xét, thay vì là toàn bộ ma trận patch của frame.

Tuy nhiên, trong paper thì tác giả chưa thử nghiệm 2 cách lấy cuối cùng, mà chỉ thử nghiệm 3 cách thử đầu tiên. Đương nhiên, cách thứ 3 sẽ ra kết quả tốt hơn cách 1 mà computational expensive không bị vượt quá như cách 2.

2.4 Benchmarking:

Mình xin phép đưa ra một vài kết quả ở trong paper ra đây. Kết quả được so sánh với các kiến trúc trước theo các tiêu chí chính: Thời gian training, yêu cầu tính toán (Inference TFLOPs), số lượng tham số (Params) và accuracy. Cho dù số lượng params rất lớn (do phải lưu trữ toàn bộ các phép tính self-attention) nhưng cả 3 tiêu chí về tốc độ, computational cost và accuracy đều cải thiện rõ rệt. Điều này càng thể hiện một cách rõ nét hơn sự hiệu quả của Transformers so với các mạng 3D-CNN truyền thống:

Hình 7. So sánh giữa các biến thể của kiến trúc mạng TimeSformer và các mạng 3D-CNN truyền thống đã được pretrained trên tập ImageNet

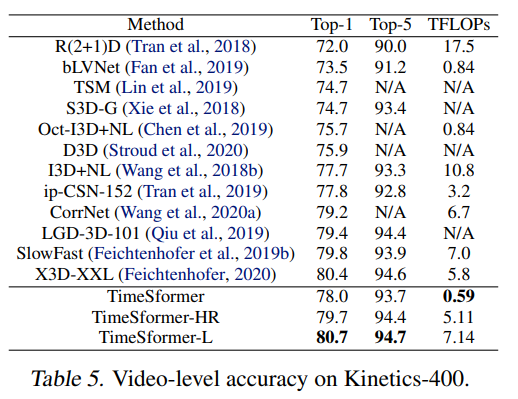
Hình 8. So sánh giữa các biến thể của kiến trúc mạng TimeSformer với các kiến trúc mạng SOTA trước đây theo accuracy và TFLOPs

3. Tổng kết:

Transformers là một kiến trúc rất mạnh mẽ, rất có tiềm năng và có thể sử dụng trong nhiều lĩnh vực. Điều này càng được chứng minh khi mà hàng loạt các bài toán CV đều có thể được giải quyết và đưa ra kết quả tốt hơn các kiến trúc mạng CNN truyền thống, điển hình như kiến trúc mạng TimeSformer mình đã trình bày. Liệu Transformers có thay thế được CNN – vốn đã thống trị các bài toán thuộc lĩnh vực CV trong suốt mấy năm vừa qua?

Bài viết chắc chắn sẽ còn nhiều thiếu sót, rất mong nhận được góp ý của mọi người để bài viết trở nên tốt hơn. Cảm ơn các bạn đã theo dõi và đọc bài của mình, nếu các bạn thấy bài viết hay thì có thể cho mình 1 upvote và 1 bookmark nha. See ya!

4. Tài liệu tham khảo:

• Is Space-Time Attention All You Need for Video Understanding?
• An Image is Worth 16×16 Words: Transformers for Image Recognition at Scale
• On Transformers, TimeSformers, and Attention (Thanks for beautiful and easy-to-understand gif pictures)