Introduction

Xin chào mọi người, trong bài viết ngày hôm này minh sẽ cùng mọi người tìm hiểu về Variational Autoencoder (VAE), một loại generative model trong deep learning. Trong vài năm gần đây, các mô hình generative đang thu hút được sự chú ý của các nhà nghiên cứu và đạt được một số kết quả đáng kinh ngạc trong một số ứng dụng như: super resolution, face generation, … Một số họ mô hình generative nổi bật có thể kể đến như Generative Adversarial Network và Variational Autoencoder.

Ở bài viết này, mình sẽ giới thiệu với mọi người về kiến trúc của VAE và cách cài đặt VAE trong thư viện Pytorch. Let’s get started!!!

Variational Autoencoder vs Autoencoder

Khi nhắc tới VAE thì chắc hẳn mọi người sẽ liên tưởng ngay tới Autoencoder. Vậy 2 mô hình này có những điểm nào giống và khác nhau? Từ “autoencoder” trong VAE ám chỉ sự giống nhau trong kiến trúc mạng giữa VAE và Autoencoder nhưng trên thực tế cả 2 lại rất khác nhau về biểu diễn toán học

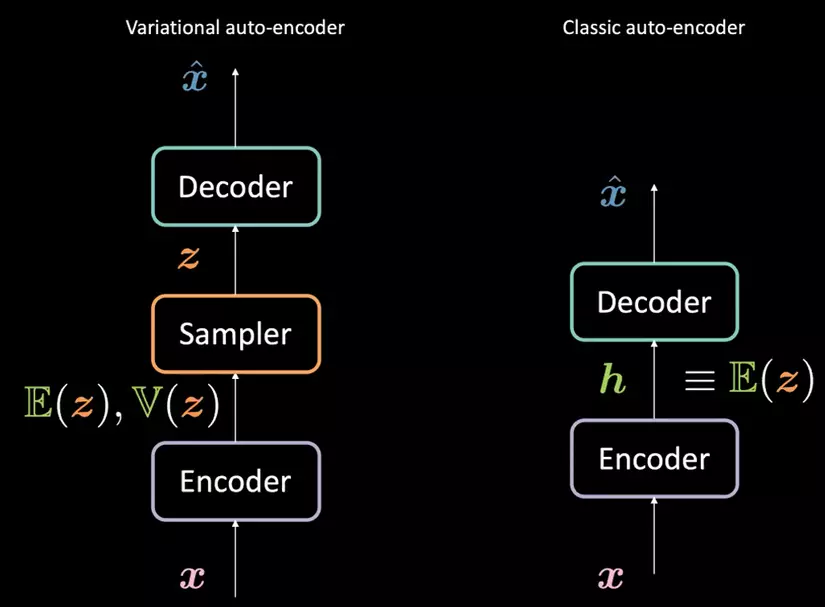
Với Autoencoder:

• Bộ encoder sẽ ánh xạ đầu vào $x$ thành một vector ẩn $h$ (thông thường với số chiều nhỏ hơn $x$) gọi là mã.
• Vector ẩn $h$ sau đó sẽ được bộ decoder biến đổi thành output của mô hình x^hat{x}x^. Output sau đó sẽ được sử dụng để tính hàm mất mát trong các tác vụ như tái cấu trúc ảnh hay denoise.

Với Variational Autoencoder:

• Quy trình cũng tương tự như với autoencoder. Nhưng thay vì ánh xạ sang 1 vector mã $h$, mã của VAE bao gồm hai vector $\mathbb{E}(z)$ và $\mathbb{V}(z)$, trong đó $z$ là một biến ngẫu nhiên có phân phối chuẩn $d$ chiều với vector trung bình $\mathbb{E}(z)$ và phương sai $\mathbb{V}(z)$. Trên thực tế và trong các paper thì các tác giả hay sử dụng phân phối chuẩn nhưng ta cũng có thể sử dụng các phân phối khác để thay thế. Bộ encoder sẽ là 1 ánh xạ f:Rdx↦R2dhf: R^{d_x} mapsto R^{2d_h}f:Rdx​↦R2dh​ (Mã $h$ của VAE sẽ là vector sau khi concat 2 vector $\mathbb{E}(z)$ và $\mathbb{V}(z)$)
• Từ 2 vector $\mathbb{E}(z)$ và $\mathbb{V}(z)$, một vector ẩn $z$ sẽ được sample từ phân chuẩn có trung bình và phương sai tương ứng.
• Vector $z$ sau đó sẽ được decoder biến đổi thành x^hat xx^.

Thay vì ánh xạ đầu vào $x$ thành 1 điểm duy nhất trong không gian ẩn như trong autoencoder, VAE ánh xạ $x$ thành một phân phối xác suất để từ đó sample $z$ từ không gian ẩn để đưa qua decoder. Vì thế, không gian ẩn của VAE được ràng buộc thành 1 không gian trơn, liên tục giúp thuận lợi cho việc sinh ra ảnh mới.

Loss function

Hàm loss của Variational autoencoder gồm 2 thành phần: reconstruction loss và regularization loss:

L(x,x^)=lreconstruct+βKL(z,N(0,Id))L(x, hat x) = l_{reconstruct} + betabold{KL}(z, N(0, I_d))
L(x,x^)=lreconstruct​+βKL(z,N(0,Id​))

• Reconstruction loss: dùng để reconstruct lại input ban đầu. Các hàm loss thông dụng là Mean Square Error hay Mean Absolute Error. Trong trường hợp ảnh nhị phân, ta có thể sử dụng binary cross entropy
• Regulization loss: sử dụng KL divergence (khoảng cách giữa 2 phân phối xác suất) giữa phân phối chuẩn với trung bình $\mathbb{E}(z)$ và phương sai $\mathbb{V}(z)$ với phân phối chuẩn chuẩn tắc $d$ chiều N(0,Id)N(0, I_d)N(0,Id​)

KL(z,N(0,Id))=12∑i=1d(V(zi)−log⁡V(zi)−1+E(zi)2)bold{KL}(z, N(0, I_d)) = frac{1}{2}sum_{i=1}^d( mathbb V(z_i) – log mathbb V(z_i) – 1 + mathbb E(z_i)^2)
KL(z,N(0,Id​))=21​i=1∑d​(V(zi​)−logV(zi​)−1+E(zi​)2)

Reparameterization trick

Như mọi người đều biết, để huấn luyện một mô hình học sâu thì ta cần tới thuật toán gradient descent, mà muốn thực hiện gradient descent thì phải có đạo hàm. Trong Variational autoencoder, thì ta có một bước sample từ phân phối chuẩn để thu được vector ẩn $z$ để đưa qua decoder. Tuy nhiên, có 1 vấn đề nho nhỏ là làm sao ta lan truyền ngược qua module sampling này để tính đạo hàm.

Thay vì trực tiếp sample từ phân phối xác suất, ta sử dụng 1 mẹo nhỏ gọi là reparameterization. Vector $z$ sẽ được tính bằng công thức

z=E(z)+ϵ⊙V(z)z = mathbb E(z) + epsilon odot sqrt{mathbb V(z)}
z=E(z)+ϵ⊙V(z)​

trong đó ϵ∼N(0,Id)epsilon sim N(0, I_d)ϵ∼N(0,Id​). Do $\mathbb{E}(z)$ và $\mathbb{V}(z)$ là outout của encoder nên đạo hàm có thể lan truyền ngược lên.

Implementation

Ở phần này mình sẽ cài đặt thử Variational autoencoder với bộ dữ liệu MNIST

Encoder và decoder

classVAE(nn.Module):def__init__(self, encoder, decoder, d=64):super().__init__()
        
        self.encoder = nn.Sequential(
            nn.Linear(784, d *8),
            nn.ReLU(),
            nn.Linear(d *8, d *4),
            nn.ReLU(),
            nn.Linear(d *4, d *2))

        self.decoder = nn.Sequential(
            nn.Linear(d, d *4),
            nn.ReLU(),
            nn.Linear(d *4, d *8),
            nn.ReLU(),
            nn.Linear(d *8,784),
            nn.Sigmoid(),)defforward(self, x):
        mu_logvar = self.encoder(x.view(-1,784)).view(-1,2, d)
        mu = mu_logvar[:,0,:]
        logvar = mu_logvar[:,1,:]
        z = self.reparameterise(mu, logvar)return self.decoder(z), mu, logvar

Reparameterisation: trong hàm reparameterise ta sử dụng log của variance để quá trình training ổn định hơn

defreparameterise(self, mu, logvar):if self.training:
        std = logvar.mul(0.5).exp_()
        epsilon = std.data.new(std.size()).normal_()return epsilon.mul(std).add_(mu)else:return mu

Hàm Loss

def loss_function(x_hat, x, mu, logvar, beta=1):
    bce = nn.functional.binary_cross_entropy(
        x_hat, x.view(-1, 784), reduction='sum'
    )
    KLD = 0.5 * torch.sum(logvar.exp() - logvar - 1 + mu.pow(2))

    return bce + beta * KLD

Và cuối cùng là training

train_loader = torch.utils.data.DataLoader(
    MNIST('./data', train=True, download=True,
                   transform=transforms.ToTensor()),
    batch_size=256, shuffle=True)
epochs =20for epoch inrange(0, epochs +1):
        model.train()
        train_loss =0for x, _ in train_loader:
            x = x.to(device)
            x_hat, mu, logvar = model(x)
            loss = loss_function(x_hat, x, mu, logvar)
            train_loss += loss.item()
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()

Sau khi huấn luyện mô hình, để sinh ra ảnh mới, ta chỉ cần sample từ phân phối chuẩn d chiều và cho qua decoder

defdisplay_images(out, n=1):for N inrange(n):
        out_pic = out.data.cpu().view(-1,28,28)
        plt.figure(figsize=(8,4))for i inrange(4):
            plt.subplot(1,4,i+1)
            plt.imshow(out_pic[i+4*N])
            plt.axis('off')
N =16
z = torch.randn((N, d)).to(device)
sample = model.decoder(z)
display_images(sample, N //4)

References

• https://atcold.github.io/NYU-DLSP21/
• https://viblo.asia/p/tim-hieu-ve-autoencoder-oOVlYvJv58W