Giới thiệu

Hôm nay mình sẽ giới thiệu đến các bạn một loại cấu trúc dữ liệu cuối cùng trong danh series Cấu trúc dữ liệu và giải thuật của mình là Graph.
Đồ thị là một trong những loại cấu trúc dữ liệu hữu ích nhất và sử dụng nhiều nhất trong khoa học máy tính khi nói đến mô hình hoá cuộc sống thực.
Đây là hình ảnh của một Graph đơn giản.
Tóm lại, Graph là một tập hợp các giá trị có liên quan theo kiểu cặp đôi và bạn có thể thấy ở đây chúng trông giống như một mạng nhỏ.

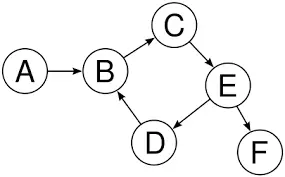
Một đồ thị gồm 2 thành phần chính :

• Các nút(Vertex) hay còn gọi là các đỉnh.Như hình trên ta có các đỉnh A, B, C, D, E, F.
• Các cạnh(Edge) : A->B, B->C, C->E, E->F, E->D, D->B.

Và như các bạn thấy, Graph là một CTDL hoàn hảo để mô phỏng các mối quan hệ trong cuộc sống thực. Ví dụ như bản đồ, các địa điểm hay thành phố là các đỉnh(Vertex), đường đi giữa các điểm là các cạnh(Edge), hay mối quan hệ trong gia đình, mỗi người là một đỉnh, còn mối quan hệ giữa họ là cạnh…

Phân loại đồ thị

Để phân loại một đồ thị, chúng ta cần xem qua các yếu tố chính để phân loại đồ thị. Có 3 yếu tố chính:

1. Đồ thị có hướng (directed) hay đồ thị vô hướng(undirected).
2. Đồ thị có trọng số (weighted) hay không có trọng số (unweighted).
3. Đồ thị có chu trình (cyclic) hay đồ thị không có chu trình (acyclic).

Directed và Undirected

Nhìn hình vẽ chúng ta có thể thấy được sự khác nhau đó là các cạnh (edges) của đồ thị có hướng sẽ có thêm mũi tên chỉ hướng ở các cạnh của đồ thị, biểu hiện chiều liên kết giữa các đỉnh của đồ thị có hướng.
Đồ thị vô hướng thì ngược lại, các cạnh sẽ không có mũi tên chỉ hướng, biểu thị tất cả liên kết của đồ thị vô hướng là hai chiều.

Ví dụ như khi ta sử dụng Facebook, mỗi một mối quan hệ bạn bè (friends) giữa những users sẽ được biểu diễn bằng đồ thị vô hướng, tức là nếu A là bạn của B thì B cũng là bạn của A. Trong khi mối quan hệ theo dõi (follow) thì lại được biểu hiện bằng đồ thị có hướng, nếu A theo dõi B thì chưa chắc B đã theo dõi lại A.

Weighted và Unweighted

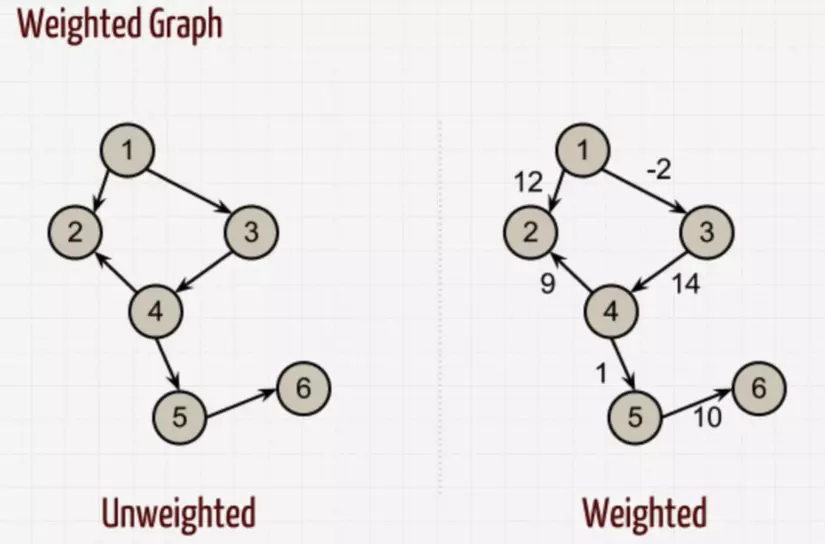
Tương tự nhìn vào hình vẽ, chúng ta cũng có thể thấy được sự khác biệt của hai loại đồ thị này, đó là đồ thị có trọng số thì mỗi cạnh của đồ thị sẽ có thêm trọng số của cạnh đó, còn ngược lại, đồ thị không có trọng số thì không có điều đó.

Trọng số mỗi cạnh sẽ có tác dụng đánh giá mức độ, độ nặng của mối liên kết giữa các nút với nhau. Ví dụ đồ thị trọng số có thể áp dụng trong việc tìm đường đi ngắn nhất trên ứng dụng bản đồ. Khi mà đi từ điểm A đến điểm C có thể qua nhiều điểm khác với trọng số (có thể là thời gian, quãng đường khác nhau) thì sẽ có kết quả khác nhau…

Cyclic và Acyclic

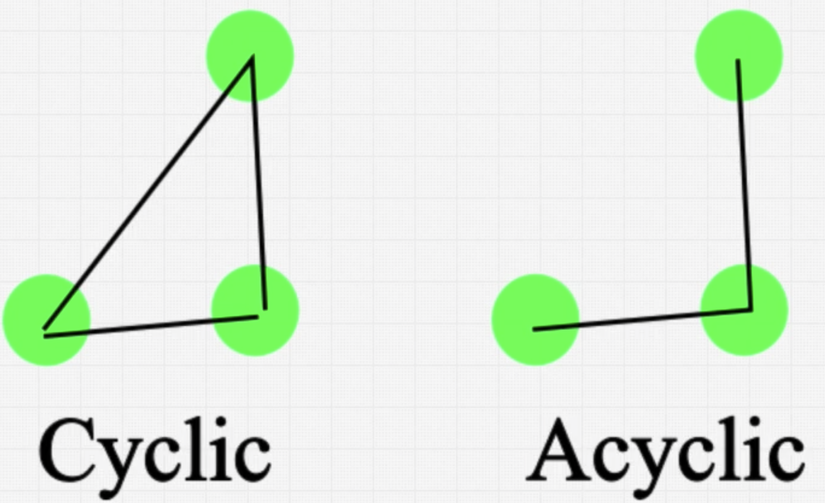
Cuối cùng là đồ thị có chu trình và đồ thị không có chu trình, đồ thị có chu trình là đồ thị mà có đường đi từ điểm A và có thể quay lại về điểm A. Đồ thị không có chu trình thì ngược lại, không có một vòng khép kín khi đi từ một điểm để quay lại điểm đó.

Implement

Đầu tiên chúng ta cùng xem một đồ thị

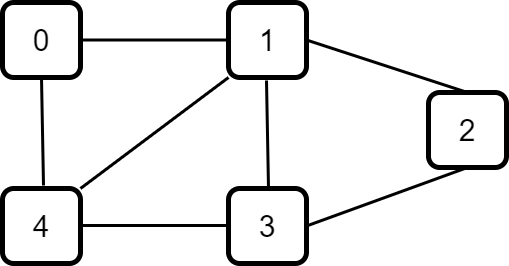
Chúng ta có vài cách để biểu thị một đồ thị như trên:

1. Dùng danh sách các cạnh (Edge List)

 // Edge List
  const graph = [[0,1],[0,4],[1,2],[1,3],[1,4],[2,3],[3,4]];

Nhìn vào đoạn code trên, ta có thể đơn giản chỉ là biểu diễn mỗi liên hệ các nút [0,1] ,[0,4] … từ đó ta có suy ra có các đỉnh 0,1, 2, 3, 4 và các liên kết giữa chúng.

2. Dùng danh sách đỉnh và các đỉnh liền kề (Adjacent List)

// Adjacent List
  const graph = {
    0: [1, 4],
    1: [0, 2, 3, 4],
    2: [1, 3],
    3: [1, 2, 4],
    4: [0, 1, 3]
  };

Nhìn vào đoạn code trên, ta thấy được sẽ có các đỉnh là 0, 1, 2, 3 ,4 và các đỉnh liên kết với nó.

3. Sử dụng ma trận đồ thị (Adjacent Matrix)

// Adjacent Matrix
  const graph = [
    [0, 1, 0, 0, 1],
    [1, 0, 1, 1, 1],
    [0, 1, 0, 1, 0],
    [0, 1, 1, 0, 1],
    [1, 1, 0, 1, 0]
  ];

Nhìn vào ma trận trên, các điểm[0,1]hay [0,4] có giá trị bằng 1 tức là có liên kết giữa 0-1 và 0-4.

Sau khi tìm hiểu các cách biểu thị các cách biểu thị đồ thị, bây giờ chúng ta cùng bắt tay implement một đồ thị không có trọng số với cách thứ 2 (Adjacent List). Với các cách khác các bạn làm tương tự nhé

class Graph {
  Map<int, List<int>> adjacentList = {};

  void addVertex(int node) {
    adjacentList.putIfAbsent(node, () => []);
  }

  void addEdge(int node1, int node2) {
    // undirected graph
    adjacentList[node1]?.add(node2);
    adjacentList[node2]?.add(node1);
  }
}

Cũng khá đơn giản đúng không, chúng là có một adjacentList để lưu dữ liệu, mỗi khi thêm một nút ta sẽ thêm một nút vào danh sách đó. Khi thêm một liên kết, ta sẽ thêm vào cả 2 node (do ở đây mình implement một đồ thị vô hướng).

Tổng kết

Như mọi khi, mình sẽ đánh giá ưu nhược điểm của CTDL, tuy nhiên với Graph thì khá là phức tạp khi nói tới độ phức tạp hay thời gian thực hiện một hành động do có rất rất nhiều loại đồ thị khác nhau. Tuy nhiên chúng ta có thể thấy chúng thật sự hữu ích khi nói đến các mối quan hệ và không thể thiếu vì một số loại dữ liệu chỉ cần ở dạng biểu đồ và không có cách nào khác. Chúng ta cũng sẽ gặp lại chúng trong các bài toán tìm đường đi ngắn nhất hay duyệt biểu đồ sau này…

Cuối cùng, thì mình rất vui vì đã cùng các bạn trải qua tìm hiểu về các loại CTDL cơ bản, hi vọng các bạn đã thu được những kiến thức có ích sau những bài viết này của mình.

Bài trước : Trees

Bài sau

Link source code