3.7 Doubly Linked Lists

Ưu điểm của doubly linked list – danh sách liên kết kép (còn được gọi là danh sách liên kết hai chiều) là với một nút trong danh sách, chúng ta có thể điều hướng theo cả hai hướng.
Không thể xóa một nút trong singly linked list trừ khi chúng ta có con trỏ tới nút phía trước của nó.
Nhưng trong danh sách được liên kết kép, chúng ta có thể xóa một nút ngay cả khi chúng ta không có địa chỉ của nút trước đó (vì mỗi nút có một con trỏ bên trái trỏ đến nút trước đó và có thể di chuyển ngược lại).
Những nhược điểm chính của danh sách được liên kết kép là:

• Mỗi nút yêu cầu thêm một con trỏ, đòi hỏi nhiều không gian bộ nhớ hơn.
• Việc chèn hoặc xóa một nút mất nhiều thời gian hơn (nhiều thao tác tới con trỏ hơn).

Tương tự như một danh sách được liên kết đơn, chúng ta triển khai các hoạt động của một danh sách được liên kết kép.
Nếu bạn hiểu các thao tác danh sách liên kết đơn, thì các thao tác danh sách liên kết kép sẽ rất rõ ràng.

public class DLLNode {
	private int data;
	private DLLNode prev;
	private DLLNode next;

	public DLLNode(int data) {
		this.data = data;
		prev = null;
		next = null;
	}

	public DLLNode(int data, DLLNode prev, DLLNode next) {
		super();
		this.data = data;
		this.prev = prev;
		this.next = next;
	}

	public int getData() {
		return data;
	}

	public void setData(int data) {
		this.data = data;
	}

	public DLLNode getPrev() {
		return prev;
	}

	public void setPrev(DLLNode prev) {
		this.prev = prev;
	}

	public DLLNode getNext() {
		return next;
	}

	public void setNext(DLLNode next) {
		this.next = next;
	}
}

Doubly Linked List Insertion

Insert vào danh sách được liên kết kép có ba trường hợp (giống như danh sách được liên kết đơn).

• Chèn một nút mới trước đầu.
• Chèn một nút mới sau đuôi (ở cuối danh sách).
• Chèn một nút mới vào giữa danh sách.

Inserting a Node in Doubly Linked List at the Beginning

Trong trường hợp này, nút mới được chèn trước nút đầu. Con trỏ trước đó và con trỏ tiếp theo cần được sửa đổi và có thể thực hiện theo hai bước:

• Cập nhật con trỏ bên phải của nút mới để trỏ đến nút đầu hiện tại (liên kết chấm trong hình bên dưới) và cũng tạo con trỏ bên trái của nút mới là NULL.

• Cập nhật con trỏ bên trái của nút đầu để trỏ đến nút mới và đặt nút mới làm phần đầu.

Inserting a Node in Doubly Linked List at the Ending

Trong trường hợp này, lướt qua danh sách cho đến cuối và chèn nút mới.

• Con trỏ bên phải của nút mới trỏ đến NULL và con trỏ bên trái trỏ đến cuối danh sách.

• Cập nhật con trỏ bên phải của nút cuối cùng để trỏ đến nút mới.

Inserting a Node in Doubly Linked List in the Middle

Như đã thảo luận trong các danh sách được liên kết đơn lẻ, hãy duyệt danh sách đến Position Node và chèn nút mới.

• Con trỏ bên phải của nút mới trỏ đến nút tiếp theo của nút vị trí mà chúng ta muốn chèn nút mới. Ngoài ra, con trỏ bên trái của nút mới trỏ đến Position Node.

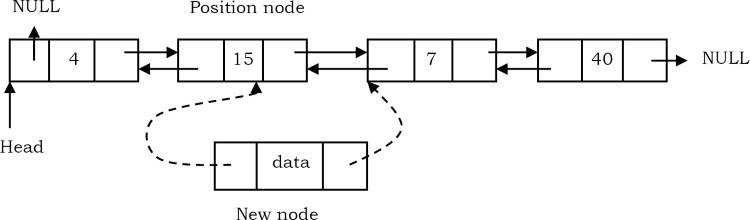
• Con trỏ bên phải Position Node trỏ đến nút mới và con trỏ trái của nút tiếp theo của Position Node trỏ đến nút mới.

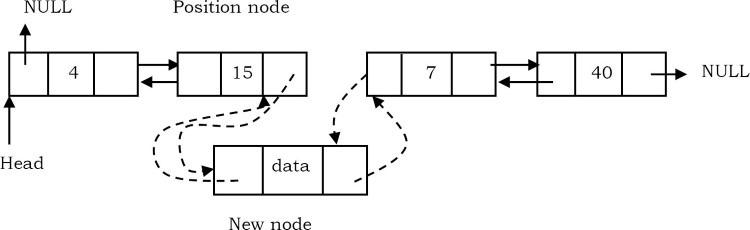
Time Complexity: $O(n)$. Trong trường hợp xấu nhất, chúng ta có thể phải chèn nút vào cuối danh sách.
Space Complexity: $O(1)$, để tạo một biến tạm thời.

Doubly Linked List Deletion

Tương tự như danh sách được liên kết đơn, ở đây chúng ta có 3 trường hợp có thể xảy ra:

• Xóa nút ở đầu.
• Xóa nút đuôi (ở cuối danh sách).
• Xóa nút vào giữa danh sách.

Deleting the First Node in Doubly Linked List

Trong trường hợp này, nút đầu tiên bị xóa khỏi danh sách. Nó có thể được thực hiện trong hai bước

• Tạo một nút tạm thời sẽ trỏ đến cùng một nút với nút của phần đầu.

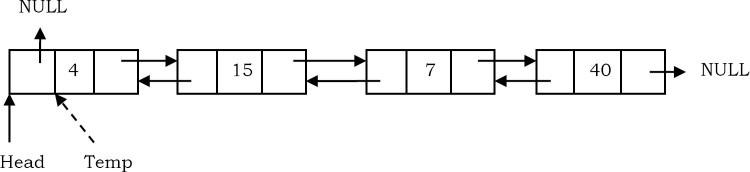
• Bây giờ, di chuyển head node sang nút tiếp theo, con trỏ trái thành null và loại bỏ nút tạm thời.

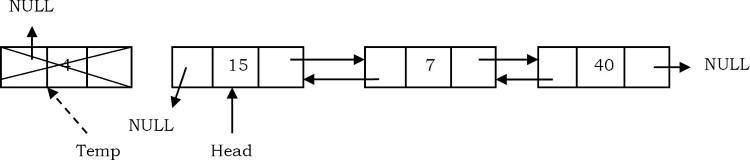
Deleting the Last Node in Doubly Linked List

Thao tác này phức tạp hơn một chút so với việc loại bỏ nút đầu tiên, bởi vì thuật toán sẽ tìm một nút, nút này nằm ở phía trước của đuôi. Điều này có thể được thực hiện trong ba bước:

• Duyệt qua danh sách và trong khi duyệt cũng duy trì địa chỉ nút trước đó. Khi đến cuối danh sách, chúng ta sẽ có hai con trỏ, một trỏ tới đuôi và một trỏ đến nút phía trước của đuôi.

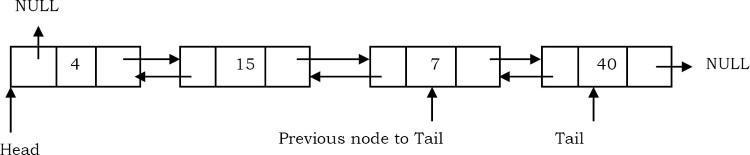
• Cập nhật con trỏ phải của nút trước đó thành nút đuôi với NULL.

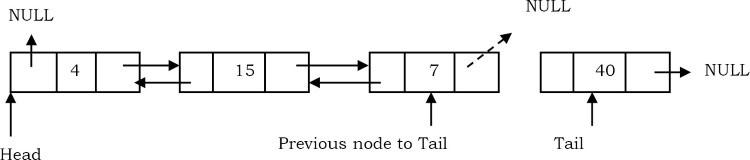
• Loại bỏ nút đuôi.

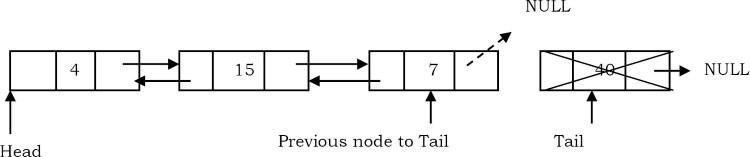
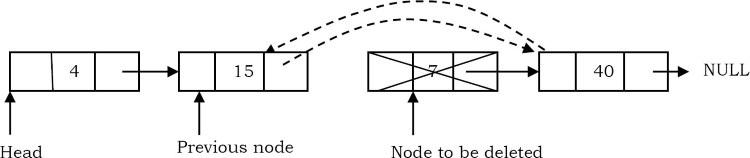
Deleting an Intermediate Node in Doubly Linked List

Trong trường hợp này, nút bị xóa luôn nằm giữa hai nút.
Việc loại bỏ có thể được thực hiện theo hai bước:

• Tương tự như trường hợp trước, duy trì nút trước trong khi cũng duyệt qua danh sách. Khi định vị nút sẽ bị xóa, hãy thay đổi con trỏ next của nút trước thành nút phía sau của nút sẽ bị xóa.

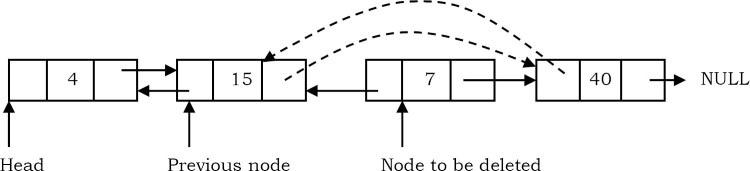
• Loại bỏ nút hiện tại

Time Complexity: $O(n)$. Trong trường hợp xấu nhất, chúng ta có thể phải chèn nút vào cuối danh sách.
Space Complexity: $O(1)$, để tạo một biến tạm thời.

Implementation

public class DoublyLinkedList {
	private DLLNode head;
	private DLLNode tail;
	private int length;

	// Create a new empty list
	public DoublyLinkedList() {
		head = new DLLNode(Integer.MIN_VALUE, null, null);
		tail = new DLLNode(Integer.MIN_VALUE, head, null);
		head.setNext(tail);
		length = 0;
	}

	// Get the value at a given position
	public int get(int position) {
		return Integer.MIN_VALUE;
	}

	// Find the position of the head value that is equal to a given value
	public int getPosition(int data) {
		DLLNode temp = head;
		int pos = 0;
		while (temp != null) {
			if (temp.getData() == data) {
				// return the position if found
				return pos;
			}
			pos++;
			temp = temp.getNext();
		}
		// else return MIN_VALUE
		return Integer.MIN_VALUE;
	}

	// Return the current length of the list
	public int length() {
		return length;
	}

	// Add a new value to the front of the list
	public void insert(int newValue) {
		DLLNode newNode = new DLLNode(newValue, null, head.getNext());
		newNode.getNext().setPrev(newNode);
		head = newNode;
		length++;
	}

	// Add a new value to the list at a given position
	// All values at that position to the end move over to make room
	public void insert(int data, int position) {
		// fix the position
		// fix position
		if (position < 0) {
			position = 0;
		}
		if (position > length) {
			position = length;
		}
		// if the list is empty, make it be the only element
		if (head == null) {
			head = new DLLNode(data);
			tail = head;
		} else {
			// if adding at the front of the list ...
			if (position == 0) {
				DLLNode temp = new DLLNode(data);
				temp.setNext(head);
				head.setPrev(temp);
				head = temp;
			}
			// else find the correct position and insert
			else {
				DLLNode temp = head;
				for (int i = 1; i < position; i++) {
					temp = temp.getNext();
				}
				DLLNode newNode = new DLLNode(data);
				newNode.setNext(temp.getNext());
				newNode.setPrev(temp);
				newNode.getNext().setPrev(newNode);
				temp.setNext(newNode);
			}
		}
		// the list is now one value longer
		length++;
	}

	// Add a new value to the rear of the list
	public void insertTail(int newValue) {
		DLLNode newNode = new DLLNode(newValue, tail.getPrev(), tail);
		newNode.getPrev().setNext(newNode);
		tail.setPrev(newNode);
		length++;
	}

	// Remove value at a given position
	// If the position is less than 0, remove the value at position 0
	// If the position is greater than 0, remove the value at last position
	public void remove(int position) {
		// fix position
		if (position < 0) {
			position = 0;
		}
		if (position >= length) {
			position = length - 1;
		}
		// if nothing in the list, do nothing
		if (head == null) {
			return;
		}
		// if removing the head element
		if (position == 0) {
			head = head.getNext();
			if (head == null) {
				tail = null;
			}
		}
		// else advance to the correct position and remove
		else {
			DLLNode temp = head;
			for (int i = 1; i < position; i++) {
				temp = temp.getNext();
			}
			temp.getNext().setPrev(temp.getPrev());
			temp.getPrev().setNext(temp.getNext());
		}
		// reduce the length of the list
		length--;
	}

	// Remove a node matching the specified node from the list
	// Use equals() instead of == to test for a matched node
	public synchronized void removeMatched(ListNode node) {
		if (head == null) {
			return;
		}
		if (node.equals(head)) {
			head = head.getNext();
			if (head == null) {
				tail = null;
			}
			return;
		}
		DLLNode p = head;
		while (p != null) {
			if (node.equals(head)) {
				p.getPrev().setNext(p.getNext());
				p.getNext().setPrev(p.getPrev());
				return;
			}
		}
	}

	// Remove the head value from the list. If the list is empty, do nothing
	public int removeHead() {
		if (length == 0) {
			return Integer.MIN_VALUE;
		}
		DLLNode save = head.getNext();
		head.setNext(save.getNext());
		save.getNext().setPrev(head);
		length--;
		return save.getData();
	}

	// Remove the tail value from the list. If the list is empty, do nothing
	public int removeTail() {
		if (length == 0) {
			return Integer.MIN_VALUE;
		}
		DLLNode save = tail.getPrev();
		head.setPrev(save.getPrev());
		save.getPrev().setNext(tail);
		length--;
		return save.getData();
	}

	// Retrun a string representation of this collection in the form ["str1",
	// "str2", ...]
	public String toString() {
		String result = "[]";
		if (length == 0) {
			return result;
		}
		result = "[" + head.getNext().getData();
		DLLNode temp = head.getNext().getNext();
		while (temp != tail) {
			result += "," + temp.getData();
			temp = temp.getNext();
		}
		return result + "]";
	}
	
	//Remove everything from the list
		public void clearList() {
			head = null;
			tail = null;
			length = 0;
		}
}