Problem-54
public int isPrime(int n) {
for(int i=2; i <= Math.sqrt(n); i++) {
if(n%i == 0) {
System.out.println("Not Prime");
return 0;
}
}
return 1;
}
Cho function sau, ý nào sau đây là đúng:
- T(n)=O(n)T ( n ) = O ( sqrt { n } ) và T(n)=Ω(n)T ( n ) = Omega ( sqrt { n } )
- T(n)=O(n)T ( n ) = O ( sqrt { n } ) và T(n)=Ω(1)T ( n ) = Omega ( 1 )
- T(n)=O(n)T ( n ) = O ({ n } ) và T(n)=Ω(n)T ( n ) = Omega ( sqrt { n } )
- Không đáp án nào ở trên
Solution: Ký hiệu Big O mô tả giới hạn trên chặt chẽ và ký hiệu Big Omega mô tả giới hạn dưới chặt chẽ cho một thuật toán.
Vòng lặp for trong câu hỏi được chạy tối đa nsqrt { n } lần và tối thiểu 1 lần. Vì vậy, T(n)=O(n)T ( n ) = O ( sqrt { n } ) và T(n)=Ω(1)T ( n ) = Omega ( 1 )
Problem-55
public int gcd(int n, int m) {
if(n%m == 0) return m;
n = n%m;
return gcd(m,n);
}
Cho đoạn code sau với n >=m, tìm độ phức tạp của bài toán.
- Θ(log2n)Theta ( l o g _ { 2 } ^ { n } )
- Ω(n)Omega ( n )
- Θ(log2log2n)Theta ( l o g _ { 2 } l o g _ { 2 } ^ { n } )
- Θ(n)Theta ( n )
Solution: Không có lựa chọn nào là chính xác.
Giả sử m = 2 và với mọi n = 2 i, thời gian chạy là O (1), điều này mâu thuẫn với mọi lựa chọn.
Problem-56
Giả sử T(n)=2T(n/2)+n,T(0)=T(1)=1T(n) = 2T(n/2) + n, T(0)=T(1)=1. Lựa chọn nào dưới đây là sai
- T(n)=O(n2)T ( n ) = O ( n ^ { 2 } )
- T(n)=Θ(nlogn)T ( n ) = Theta ( n log n )
- T(n)=Ω(n2)T ( n ) = Omega ( n ^ { 2 } )
- T(n)=O(nlogn)T ( n ) = O ( n log n )
Solution:
Ký hiệu Big O mô tả giới hạn trên chặt chẽ và ký hiệu Big Omega mô tả giới hạn dưới chặt chẽ cho một thuật toán.
Dựa vào master theorem , ta có
T(n)=Θ(nlogn)T ( n ) = Theta ( n log n ). Nó đồng nghĩa với Big O và Big Omega là như nhau, (2) và (4) đúng.
Problem-57
Tìm độ phức tạp:
public void function(int n) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < i*i; j++) {
if(j%i == 0) {
for(int k = 0; k < j; k++) {
System.out.println("*");
}
}
}
}
}
Solution:
Xem xét comment:
public void function(int n) {
for (int i = 0; i < n; i++) { //Vòng lặp này thực thi n lần
for (int j = 0; j < i*i; j++) { //Vòng lặp này thực thi n*n lần
if(j%i == 0) {
for(int k = 0; k < j; k++) {//Vòng lặp này thực thi j=n*n lần
System.out.println("*");
}
}
}
}
}
Time Complexity: O(n5)O(n^5).
Đây là solution mà tác giả giải thích trong sách, mình thấy có vẻ chưa chuẩn lắm, mình sẽ giải thích lại theo ý mình hiểu(Mọi người nếu thấy mình giải thích chưa đúng comment giúp để mình sửa lại nhé):
public void function(int n) {
for (int i = 0; i < n; i++) { //Vòng lặp này thực thi n lần
for (int j = 0; j < i*i; j++) { //Vòng lặp này thực thi i*i lần
if(j%i == 0) {
for(int k = 0; k < j; k++) {//Vòng lặp này thực thi j=i*i lần
System.out.println("*");
}
}
}
}
}
Vậy ta có T(n)=∑i=1ni4T ( n ) = sum _ { i = 1 } ^ { n } i^4. Áp dụng công thức cuối cùng trong bài này, ta được T(n)=(1/(4+1))∗n5=O(n5)T(n) = (1/(4 + 1)) * n^5 = O(n^5)
Problem-58
Để tính toán 9n9^n, hãy đưa ra một thuật toán và thảo luận về độ phức tạp của nó.
Solution:
Bắt đầu với 1 và nhân với 9 cho đến khi đạt 9n9^n.
Time Complexity: Có n-1 phép nhân và mỗi phép nhân cần thời gian không đổi để thực thi => Θ(n)Θ(n)
Problem-59
Đối với Bài toán-58, chúng ta có thể cải thiện độ phức tạp về thời gian không?
Solution: Có, chi tiết mình sẽ trình ở chương Divide and Conquer.
Problem-60
Tìm độ phức tạp
public void function(int n) {
int sum = 0;
for(int i = 0; i < n; i++) {
if(i > j) {
sum += 1;
} else {
for(int k = 0; k < n; k++) {
sum -= 1;
}
}
}
}
Solution:
Xem xét trường hợp tệ nhất worst-case
public void function(int n) {
int sum = 0;
for(int i = 0; i < n; i++) { //Vòng lặp này thực thi n lần
if(i > j) {
sum += 1; //Lệnh này thực thi n lần
} else {
for(int k = 0; k < n; k++) {//Vòng lặp này thực thi n lần
sum -= 1;
}
}
}
}
Time Complexity: Trường hợp tệ nhất vòng lặp luôn vào else => O(n2)O(n^2)
Problem-61
Giải quan hệ lặp lại sau bằng phương pháp cây đệ quy: T(n)=T(n2)+T(2n3)+n2T ( n ) = T ( frac { n } { 2 } ) + T ( frac { 2 n } { 3 } ) + n ^ { 2 }
Solution: Câu hỏi đặt ra là: chúng ta thực hiện bao nhiêu công việc trong mỗi cấp của cây đệ quy?
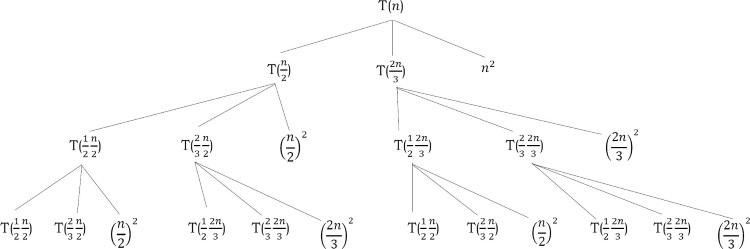
Ở mức 0, chúng ta mất n2n^2 lần.
Ở mức 1, chia thành 2 vấn đề con cần: (12n)2+(23n)2=(14+49)n2=(2536)n2left ( frac { 1 } { 2 } n right ) ^ { 2 } + left ( frac { 2 } { 3 } n right ) ^ { 2 } = left ( frac { 1 } { 4 } + frac { 4 } { 9 } right ) n ^ { 2 } = left ( frac { 2 5 } { 36 } right ) n ^ { 2 }
Ở mức 2, chia thành 4 vấn đề con với zize 12frac { 1 } { 2 }n2frac { n } { 2 }, 23frac { 2 } { 3 }n2frac { n } { 2 }, 12frac { 1 } { 2 }2n3frac { 2n } { 3 } và 23frac { 2 } { 3 }2n3frac { 2n } { 3 }, 2 vấn đề con cần:
(14n)2+(13n)2+(13)n2+(49)n2=(6251296)n2=(2536)2n2left ( frac { 1 } { 4 } n right ) ^ { 2 } + left ( frac { 1 } { 3 } n right ) ^ { 2 } + left ( frac { 1 } { 3 } right )n ^ { 2 } + left ( frac { 4 } { 9 } right ) n^ { 2 } = left ( frac { 625 } { 1296 } right ) n ^ { 2 } = left ( frac { 2 5 } { 36 } right )^2 n ^ { 2 }
Tương tự khối lượng công việc ở cấp độ k tối đa là (2536)kn2(frac { 2 5 } { 36 }) ^k n ^ { 2 }
Đặt α=2536alpha = frac { 2 5 } { 3 6 }, tổng runtime cần là:
T(n)≤∑k=0∞αkn2T ( n ) leq sum _ { k = 0 } ^ { infty } alpha ^ { k } n ^ { 2 }
=11−αn2= frac { 1 } { 1 – alpha } n ^ { 2 }
=11−2536n2= frac { 1 } { 1 – frac { 2 5 } { 3 6 } } n ^ { 2 }
=11136n2= frac { 1 } { frac { 1 1 } { 3 6 } } n ^ { 2 }
=3611n2= frac { 3 6 } { 1 1 } n ^ { 2 }
=O(n2)= O ( n ^ { 2 } )
Problem-62
Tìm độ phức tạp: T(n)=T(n2)+T(n4)+T(n8)+nT ( n ) = T ( frac { n } { 2 } ) + T ( frac { n } { 4 } ) + T ( frac { n } { 8 } ) + n
Solution:
Chúng ta thử giải quyết vấn đề bằng phương pháp guessing. Ta thấy tổng kích thước trên mỗi level lặp lại đều nhỏ hơn n, vậy ta đoán rằng f(n)=nf(n) = n sẽ chiếm ưu thế.
Giả sử với mọi i < n thì c1n≤T(i)≤c2nc _ { 1 } n leq T ( i ) leq c _ { 2 } n, ta được:
c1n2+c4n4+c1n8+kn≤T(n)≤c2n2+c2n4+knc _ { 1 } frac { n } { 2 } + c _ { 4 } frac { n } { 4 } + c _ { 1 } frac { n } { 8 } + kn leq T ( n ) leq c _ { 2 } frac { n } { 2 } + c _ { 2 } frac { n } { 4 } + k n
<=>c1n(12+14+18+kc1)+≤T(n)≤c2n(12+14+18+kc2)<=>c _ { 1 } n ( frac { 1 } { 2 } + frac { 1 } { 4 } + frac { 1 } { 8 } + frac { k } { c1 } ) + leq T ( n ) leq c _ { 2 } n ( frac { 1 } { 2 } + frac { 1 } { 4 } + frac { 1 } { 8 } + frac { k } { c2 } )
<=>c1n(78+kc1)≤T(n)≤c2n(78+kc2)<=>c _ { 1 } n ( frac { 7 } { 8 } + frac { k } { c _ { 1 } } ) quad leq T ( n ) quad leq quad c _ { 2 } n ( frac { 7 } { 8 } + frac { k } { c _ { 2 } } )
Nếu c1≥8kc1 geq 8k và c2≤8kc2 leq 8k thì c1n=T(n)=c2nc _ { 1 } n = T(n) =c _ { 2 } n, như vậy T(n)=Θ(n)T(n) = Θ(n).
Kết luận: nếu ta có nhiều lệnh gọi đệ quy, tổng các đối số của các lệnh gọi đó nhỏ hơn n(trong trường hợp này n2+n4+n8<nfrac { n } { 2 } + frac { n } { 4 } + frac { n } { 8 } < n), và f(n) đủ lớn thì một dự đoán tốt là T(n)=Θ(n)T(n) = Θ(n).
Problem-63
Xếp hạng các chức năng sau theo thứ tự rate of growth:
![]()
Solution:

Problem-64
Ta có thể nói 3n0.75=O(3n)3 ^ { n ^ { 0 . 7 5 } } = O ( 3 ^ { n } ) ?
Solution: Yes, bởi vì 3n0.75<3n13 ^ { n ^ { 0 . 7 5 } } < 3 ^ { n ^ { 1 } }
Problem-65
Ta có thể nói 23n=O(2n)2 ^ { 3 n } = O ( 2 ^ { n } ) ?
Solution: Không, bởi vì 23n=(23)n=8n2 ^ { 3 n } = ( 2 ^ { 3 } ) ^ { n } = 8 ^ { n } không nhỏ hơn 2n2^n.
Kết chương 1
Cảm ơn mọi người đã đọc tới đây, vậy là mình đã trình bày xong toàn bộ lý thuyết và bài tập của chương 1. Chương này khá khó và sử dụng nhiều kiến thức toán, bắt đầu từ chương sau sẽ đi vào các bài toán cụ thể và sẽ được áp dụng code nhiều hơn 😁😁😁
Nguồn: viblo.asia
