Từ đây tới chương 2 sẽ là các bài viết về bài tập nhằm giúp các bạn hiểu hơn về những lý thuyết đã qua.
Để không quá dài, mình sẽ chỉ để khoảng từ 8-10 bài tập mỗi bài viết.
Problem-21
Tìm độ phức tạp của hàm đệ quy:
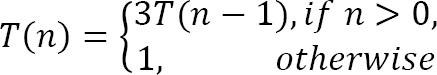
Solution: Chúng ta hãy thử giải quyết function này bằng cách substitution(thay thế):
T(n)=3T(n−1)T ( n ) = 3 T ( n – 1 )
T(n)=3(3T(n−2))=32T(n−2)T ( n ) = 3 ( 3 T ( n – 2 ) ) = 3 ^ { 2 } T ( n – 2 )
T(n)=32(3T(n−3))T ( n ) = 3 ^ { 2 } ( 3 T ( n – 3 ) )
…
T(n)=3nT(n−n)=3nT(0)=3nT ( n ) = 3 ^ { n } T ( n – n ) = 3 ^ { n } T ( 0 ) = 3 ^ { n }
Điều này cho thấy rõ ràng rằng độ phức tạp của hàm này là O(3n)O ( 3 ^ { n } ).
Note: Chúng ta cũng có thể sử dụng các định lý về Subtraction and Conquer cho bài toán này.
Problem-22
Tìm độ phức tạp của hàm đệ quy:
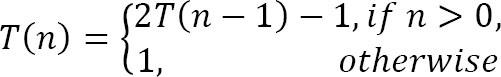
Solution: Chúng ta hãy thử giải quyết function này bằng cách substitution(thay thế):
T(n)=2T(n−1)−1T ( n ) = 2 T ( n – 1 ) – 1
T(n)=2(2T(n−2)−1)−1=22T(n−2)−2−1T ( n ) = 2 ( 2 T ( n – 2 ) – 1 ) – 1 = 2 ^ { 2 } T ( n – 2 ) – 2 – 1
T(n)=22(2T(n−3)−2−1)=23T(n−4)−22−21−20T ( n ) = 2 ^ { 2 } ( 2 T ( n – 3 ) – 2 -1 ) = 2 ^ { 3 } T ( n – 4 ) – 2 ^ { 2 } – 2 ^ { 1 } – 2 ^ { 0 }
T(n)=2nT(n−n)−2n−1−2n−2−2n−3 . . . 22−21−20T ( n ) = 2 ^ { n } T ( n – n ) – 2 ^ { n – 1 } – 2 ^ { n – 2 } – 2 ^ { n – 3 } text { . . . } 2 ^ { 2 } – 2 ^ { 1 } – 2 ^ { 0 }
T(n)=2n−2n−1−2n−2−2n−3− . . . 22−21−20T ( n ) = 2 ^ { n } – 2 ^ { n – 1 } – 2 ^ { n – 2 } – 2 ^ { n – 3 }- text { . . . } 2 ^ { 2 } – 2 ^ { 1 } – 2 ^ { 0 }
T(n)=2n−(2n−1)[note:2n−1+2n−2+⋯+20=2n−1]T ( n ) = 2 ^ { n } – ( 2 ^ { n } – 1 ) [ n o t e: 2 ^ { n – 1 } + 2 ^ { n – 2 } + cdots + 2 ^ { 0 } = 2 ^ { n } – 1]
T(n)=1T ( n ) = 1
=> Complexity là O(1)O ( 1 ).
Problem-23
Xác định running time của function sau:
public void Funtion(int n) {
int i = 1, s = 1;
while(s <= n) {
i++;
s = s + i;
System.out.println("*");
}
}
Ta có thể xác định ′s′^ { prime }s ^ { prime } theo quan hệ si=si−1+is _ { i } = s _ { i – 1 } + i với giá trị của ′i′^ { prime }i ^ { prime } tăng 1 sau mỗi vòng lặp.
Giá trị chứa trong ‘s’ ở lần lặp thứ i là tổng của các số nguyên dương ‘i’ đầu tiên.
Giả sử k là tổng số lần lặp được thực hiện bởi chương trình, thì vòng lặp while kết thúc nếu:
s=1+2+…+k=k(k+1)2>n⇒k=O(n)s = 1 + 2 + ldots + k = frac { k ( k + 1 ) } { 2 } > n Rightarrow k = O ( sqrt { n } )
Problem-24
Xác định running time của function sau:
public void Funtion(int n) {
int i = 1, count = 0;
for (i = 0; i*i <= n; i++) {
count++;
}
}
Solution:
Trong hàm được đề cập ở trên, vòng lặp sẽ kết thúc, nếu i2>n=>T(n)=O(n)i ^ { 2 } > n => T ( n ) = O ( sqrt { n } ). Tương tự Problem-23
Problem-25
Xác định running time của function sau:
public void Funtion(int n) {
int i,j,k, count = 0;
for(i = n/2; i <= n; i++){
for(j = n/2; j <= n; j++){
for(k = n/2; k <= n; k = k*2){
count++;
}
}
}
}
Solution: Chúng ta hãy xem lại code, mình sẽ comment chi tiết ở từng vòng lặp
public void Funtion(int n) {
int i,j,k, count = 0;
//Vòng lặp ngoài cùng thực thi n/2 lần
for(i = n/2; i <= n; i++){
//Vòng lặp giữa thực thi n/2 lần
for(j = 1; j + n/2 <= n; j++){
//Vòng lặp trong cùng thực thi logn lần
for(k = n/2; k <= n; k = k*2){
count++;
}
}
}
}
=> Complexity của function trên là O(n2logn)O ( n ^ { 2 } l o g n )
Problem-26
Xác định running time của function sau:
public void Funtion(int n) {
int i,j,k, count = 0;
for(i = n/2; i <= n; i++){
for(j = 1; j <= n; j = 2*j){
for(k = n/2; k <= n; k = k*2){
count++;
}
}
}
}
Solution: Chúng ta hãy xem lại code, mình sẽ comment chi tiết ở từng vòng lặp
public void Funtion(int n) {
int i,j,k, count = 0;
//Vòng lặp ngoài cùng thực thi n/2 lần
for(i = n/2; i <= n; i++){
//Vòng lặp giữa thực thi logn lần
for(j = 1; j <= n; j = 2*j){
//Vòng lặp trong cùng thực thi logn lần
for(k = n/2; k <= n; k = k*2){
count++;
}
}
}
}
=> Complexity của function trên là O(nlog2n)O ( n l o g^ { 2 } n )
Problem-27
Xác định running time của function sau:
public void Funtion(int n) {
if(n == 1) return;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
System.out.println("*");
break;
}
}
}
Solution: Chúng ta hãy xem lại code, mình sẽ comment chi tiết ở từng vòng lặp
public void Funtion(int n) {
//constant time
if(n == 1) return;
//Vòng lặp ngoài cùng thực thi n lần
for (int i = 1; i <= n; i++) {
//Vòng lặp trong chỉ thực thi 1 lần do lệnh break;
for (int j = 1; j <= n; j++) {
System.out.println("*");
break;
}
}
}
=> Complexity của function trên là O(n)O ( n ). Mặc dù vòng lặp bên trong có giới hạn là n, nhưng do câu lệnh break nên nó chỉ được thực thi một lần.
Problem-28
Một hàm đệ quy cho thời gian chạy T(n)T ( n ) của function cho dưới đây.
Chứng minh bằng phương pháp lặp rằng T(n)=Θ(n3)T ( n ) = Theta ( n ^ { 3 } ).
public void Funtion(int n) {
if(n == 1) return;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
System.out.println("*");
}
}
Funtion(n-3);
}
Solution: Chúng ta hãy xem lại code, mình sẽ comment chi tiết ở từng vòng lặp
public void Funtion(int n) {
//constant time
if(n == 1) return;
//Vòng lặp ngoài cùng thực thi n lần
for (int i = 1; i <= n; i++) {
//Vòng lặp trong cùng thực thi n lần
for (int j = 1; j <= n; j++) {
//constant time
System.out.println("*");
}
}
Funtion(n-3);
}
Sự lặp lại đối với mã này rõ ràng là T(n)=T(n−3)+cn2T ( n ) = T ( n – 3 ) + c n ^ { 2 } đối với một số hằng c> 0 vì mỗi lệnh gọi in ra n2n^2 dấu hoa thị và chính nó gọi đệ quy với n−3n-3. Sử dụng định lý chính Subtraction and Conquer master theorem, ta được T(n)=Θ(n3)T ( n ) = Theta ( n ^ { 3 } ).
Problem-29
Xác định giới hạn Θ cho hàm sau: T(n)=2T(n2)+nlognT ( n ) = 2 T ( frac { n } { 2 } ) + n l o g n
Solution: Sử dụng Divide and Conquer master theorem, ta được O(nlog2n)O ( n l o g ^ { 2 } n )
Problem-30
Xác định giới hạn Θ cho hàm sau: T(n)=T(n2)+T(n4)+T(n8)+nT ( n ) = T ( frac { n } { 2 } ) + T ( frac { n } { 4 } ) + T ( frac { n } { 8 } ) + n
Solution: Thay vào phương trình lặp lại, chúng ta nhận được:
T(n)≤c1∗n2+c2∗n4+c3∗n8+cn≤k∗nT ( n ) leq c 1 * frac { n } { 2 } + c 2 * frac { n } { 4 } + c 3 * frac { n } { 8 } + c n leq k * n , với k là 1 constant.
=>T(n)=O(n)T ( n ) = O ( n ).
Nguồn: viblo.asia
