Chào mừng các bạn tới series tự học Machine Learning cùng mình. Mình tên là Khang và mình đang trong quá trình ôn tập kiến thức máy học. Mục đích của mình viết series này để chia sẻ kiến thức cơ bản về máy học (ML). Trong quá trình viết bài này, mình có thường sử dụng những từ ngữ chuyên ngành bằng tiếng anh, mình mong các bạn bỏ qua. Ngoài ra, sau khi các bạn đọc bài thì có thắc mắc hay phát hiện mình có sai sót gì thì có thể comment lại ở dưới giúp mình, mình sẽ cố gắng dành thời gian giải đáp.
Trong phần 1 (Part 1) này, mình sẽ giới thiệu sơ qua về kiến thức Linear Regression và cách mình optimize Loss function bằng cách dùng Gradient Descent.
1. Machine Learning overview
Let’s get started. Vậy thì machine learning là gì ? Machine learning (Máy học) là một nhánh của AI (artificial intelligence) để tập trung vào việc sử dụng data và thuật toán của máy cho việc bắt chước con người trong việc học và cải thiện accuracy . Machine learning được dùng trong nhiều lĩnh vực như:
- Ngân hàng (Fraud Detection)
- Kinh Doanh (Stock prediction)
Phần trên này mình chỉ lược sơ qua lại kiến thức overview của Machine Learning. Còn bây giờ mình sẽ vô trọng tâm của bài hôm nay.
2. Linear Regression
Tổng quát + Ví dụ
Linear Regression chỉ là 1 công thức f(x) = ax + b bình thường trong toán học của mình với 1 giá trị của x sẽ đưa ra 1 giá trị của y. Thế nhưng, trong thực tế, có rất nhiều dữ liệu (x, y) khi ta cho x vào phương trình f(x) = ax + b, thì giá trị f(x) khác với giá trị y của dữ liệu. Đây là 1 bài toán của Supervised Learning.
Ví dụ thực tế:
Ta có phương trình f(x) = 1 + 3x và 2 dữ liệu giá trị (x, y): A(1, 4) và B(2, 5)
Lúc ta thế A vào phương trình, ta có f(1) = 1 + 3 * 1 = 4 = y => A là điểm nằm trên đường thẳng của f(x).
Thế nhưng, khi chúng ta thế B vào phương trình trên, ta có f(2) = 1 + 3 * 2 = 7 != y (y = 5)
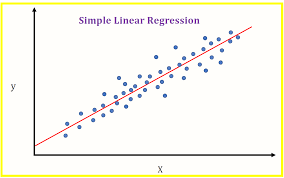
Tương tự như vậy, nếu ta có rất nhiễu dữ liệu giá trị (x, y) thì ta sẽ plot được 1 line graph dưới đây.
Trong đó:
- line (đường màu đỏ) là function f(x)
- Các chấm là dữ liệu của x và y
Qua đó, ta nhận biết được đường màu đỏ (f(x)) có thể được gọi là 1 machine learning model.
Ví dụ ở trên chỉ biểu diễn 1 function của f(x) với giá trị của y phụ thuộc vào 1 giá trị của x.
Trong trường hợp f(x) là 1 function có nhiều biến x1,x2,x3,….,xnx_1, x_2, x_3, …. , x_n
Ví dụ: Trong bài toán House Prediction như hình ở dưới
Ta thấy rằng Price phụ thuộc vào rất nhiều yếu tố như: số phòng ngủ, số nhà tắm, diện tích, etc…
Những yếu tố đó là x1,x2,x3,….,xnx_1, x_2, x_3, …. , x_n.
Từ đó, ta có công thức tổng quát của Linear Regression trong Machine Learning là:
h(x) = Θ0+Θ1∗x1+Θ2∗x2+…+Θn∗xnTheta _0 + Theta _1 * x_1 + Theta _2 * x_2 + … + Theta _n * x_n
Trong đó:
- x1−>xnx_1 -> x_n : là các giá trị tương ứng với các cột trong data
- Θ0−>ΘnTheta _0 -> Theta _n: trọng số (weights) của những giá trị tương ứng với các cột (weight càng cao thì ảnh hưởng của cột đó càng lớn)
Cách đo lường độ sai số của Linear Regression (Measure Performance)
Để đo lường độ sai số của function trong việc predict các giá trị y dựa trên nhiều biến x, ta có 1 function khác gọi là Loss Function
Loss Function: J(θ0−>θm)=(1/n)∗Σi=0n(h(xi)−yactual)2J(θ_0 -> θ_m) = (1/n) * Sigma_{i=0}^{n} (h(x^{i}) – y_{actual}) ^ 2
Trong đó:
- i: data thứ i (hàng thứ mấy)
- n: tổng data (tổng hàng row)
- h(xi)h(x^i) : giá trị dự đoán (predicted value)
- m: tổng các cột (features)
Để function h(xi)h(x^i) dự đoán được tốt nhất, chúng ta phải minimize Loss Function.
Gradient Descent
Có rất nhiều cách để minimize 1 function nói chung và Loss Function nói riêng. Nhưng trong bài này, mình chỉ đề cập tới Gradient Descent.
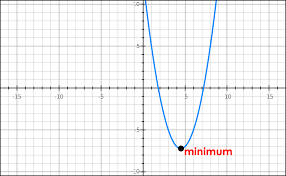
Hình bên dưới mình sẽ plot 1 graph function:
Tổng quát, thường thường thì 1 loss function sẽ được assume là convex function (hàm lõm) (có trường hợp không convex, nhưng mình không đề cập trong bài này). Thì để tìm được giá trị minimum của Loss Function, chúng ta cần phải tới (hay hội tụ) tại điểm local minimum của convex function.
 Click here to see the motion detail
Click here to see the motion detail
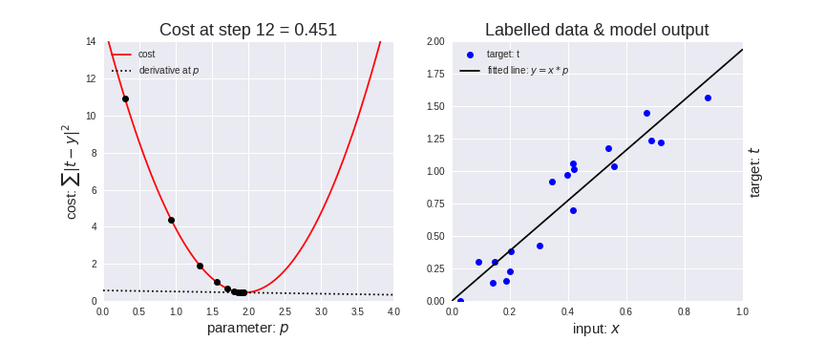
Gradient Descent tận dùng việc đạo hàm (derivatives) tại điểm bắt đầu để xác định được hướng cho bước tiếp theo (những dấu chấm đen di chuyển trên màu đỏ parabol – hình bên trái). Khi càng gần về local minimum, sự khác biệt của vị trí (giá trị) của Loss Function trước và sau khi thay đổi sẽ càng nhỏ. Khi tới được local minimum, thì đạo hàm tại đó sẽ bằng 0 đồng nghĩa với việc chúng ta đã thành công minimize được Loss Function. Nhìn hình bên phải, ta thấy đường line (function f(x)) di chuyển khi chấm đen (hình bên phải) di chuyển về phía local minimum. Từ đó ta thấy được có sự thay đổi của ΘTheta ở f(x). Sau khi minimize được Loss Function, ta sẽ có giá trị của ΘTheta. Khi đó, ta gán giá trị của
ΘTheta vào phương trình f(x) ban đầu để thực hiện việc dự đoán (Prediction).
Ở đây, mình sẽ nói các bước dùng Gradient Descent để minimize loss:
- Bước 1: Ngẫu nhiên đặt giá trị của $Theta. ( Θ0Theta_{0} – > ΘmTheta_{m} với m là tổng số features trong dataset).
- Bước 2: Thay đổi ΘjTheta_{j} ( 0 <= j <= m)
- Θj<−−Θj(old)−αTheta_{j} <- – Theta_{j (old)} – alphaδJ(Θ0−>Θm)δΘjfrac{delta J(Theta_{0} -> Theta_{m})}{delta Theta_{j}}
- Tiếp tục chạy bước 2 cho đến khi thoả mãn 2 điều kiện này:
- Thoả mãn điều kiện số iteration yêu cầu (được người dùng điền vào).
- Khi ΘjTheta_{j} và Θj(old)Theta_{j (old)} có sự khác biệt cực kì nhỏ.
Trong đó:
- Θj(old)Theta_{j (old)} : là giá trị cũ
- ΘjTheta_{j} : là giá trị mới được update
- αalpha: là learning rate
- δJ(Θ0−>Θm)δΘjfrac{delta J(Theta_{0} -> Theta_{m})}{delta Theta_{j}}: đạo hàm của Loss Function
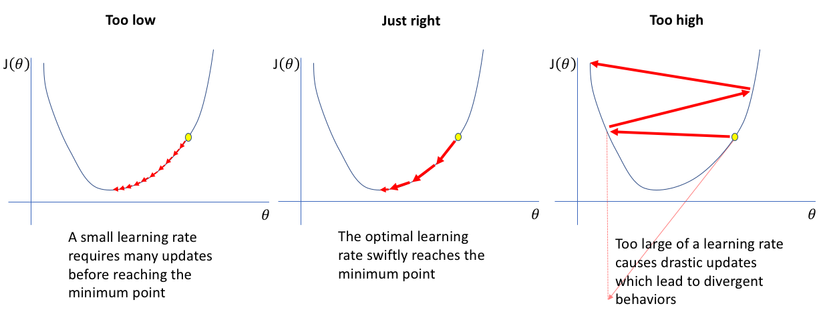
Chú ý: Learning rate αalpha
Ta chú ý trong việc chọn αalpha learning rate (nhìn hình bên dưới để dễ hình dung):
- Nếu αalpha quá nhỏ, thì quá trình hội tụ tại điểm local minimum rất là lâu.
- Nếu αalpha quá lớn, thì quá trình hội tụ tại điểm local minimum sẽ bị overshooting (nhảy qua lại, thậm chí có trường hợp không về lại được local minimum – phân kì).
3. Tổng kết
Vậy là chúng ta mới làm quen với Linear Regression và cách dùng Gradient Descent để tăng performance của Linear Regression model. Trong bài này, chúng ta cần hiểu kĩ cách hoạt động của Linear Regression model hoạt động như thế nào và cách để tăng accuracy của model. Gradient descent đã tận dụng được đạo hàm trong toán học để giúp cho quá trình hội tụ nhanh hơn. Bên cạnh đó, việc lựa chọn Learning rate αalpha cũng ảnh hưởng đến kết quả của việc tìm được local minimum trong Loss Function.
Đây là bài viết đầu tiên của mình, nếu có còn sai sót thì mong các bạn bỏ qua và comment phía dưới giúp mình để mình có thể ra được những bài chất lượng hơn trong tương lai gần. Đương nhiên là mình sẽ tiếp tục Series Study ML with me để giúp các bạn cũng như bản thân mình củng cố kiến thức Machine Learning. Mình cám ơn các bạn đã theo dõi mình tới tận đây. Peace out !
Nguồn: viblo.asia