Algorithm Introduction
In a multiprogramming environment, several threads may compete for a finite number of resources. A thread requests resources; if the resources are not available at that time, the thread enters a waiting state. Sometimes, a waiting thread can never again change state, because the resources it has requested are held by other waiting threads. This situation is called a deadlock. Generally speaking, we can deal with the deadlock problem in one of three ways:
- We can ignore the problem altogether and pretend that deadlocks never occur in the system. Called
Deadlock Prevention. - We can use a protocol to prevent or avoid deadlocks, ensuring that the system will never enter a deadlocked state. Called
Deadlock Avoidance. - We can allow the system to enter a deadlocked state, detect it, and recover. Called
Deadlock Dectection & Recovery.
Data structure for algorithm
m: the number of resource types. Resource types include R1,R2,…,RmR_{1},R_{2},…,R_{m}n: the number of threads. Threads are P1,P2,…,PnP_{1},P_{2},…,P_{n}Available: the vector of length m indicates the number of available resources of each type. For example, if Available[j]=kAvailable[j] = k, then kk instances of resource type RjR_{j} are available.Max: An n×mn times m matrix defines maximum demand of each thread. If Max[i][j]=kMax[i][j] = k, then thread PiP_{i} request at most k instances of resource type RjR_{j}.Allocation: An n×mn times m matrix defines the number of resources of each type currently allocated to each thread. If Allocation[i][j]=kAllocation[i][j] = k, then thread PiP_{i} is currently allocated k instances of resource type RjR_{j}.Need: An n×mn times m matrix indicates the remaining resource need of each thread. If Need[i][j]=kNeed[i][j] = k, then thread PiP_{i} may need kk instances of resource type RjR_{j} to complete its task. Note that Need[i][j]=Max[i][j]−Allocation[i][j]Need[i][j] = Max[i][j] – Allocation[i][j].
What is Resource-Allocation State?
Resource-Allocation State is defined by the number of instances of resources :
- available in the system
- allocated for threads
- maximum for each thread
- The system can allocate resources to each thread (up to its maximum) in some order and still avoid a deadlock.
- Exists state is safe.
- A sequence of threads is a safe sequence for the current allocation state.
For example:
Suppose that, system has 12 resources. At time t0,Allocation(P0,P1,P2)=(5,2,2)t_{0}, Allocation(P_{0},P_{1},P_{2}) = (5,2,2), Available=12−(5+2+2)=3Available = 12 – (5+2+2) = 3 resources.
| Maximum Needs | Current Needs | |
|---|---|---|
| P0P_{0} | 10 | 5 |
| P1P_{1} | 4 | 2 |
| P2P_{2} | 9 | 7 |
At time t0t_{0}, system is in safe state. Because, the sequence <P1,P0,P2><P_{1},P_{0},P_{2}> satifies the safety condition. With Available=3Available = 3 thread P1P_{1} can immediately be allocated all its resources and then return them, Available=3+2=5Available = 3 + 2 = 5; then thread P0P_{0} can get all its resources and return them, Available=5+5=10Available = 5 + 5 = 10; and finally thread T2 can get all its resources and return them.
Suppose that, at time t1t_{1} ,thread P2P_{2} requests and is allocated one more resource. At this point, only thread P1P_{1} can be allocated all its resources. When it returns them, the system will have only four available resources. Since thread P_{0) is allocated five resources but has a maximum of ten, it may request five more resources. If it does so, it will have to wait, because they are unavailable. Similarly, thread P2P_{2} may request six additional resources and have to wait, resulting in a deadlock. In this case, system go from safe state to unsafe state.
Safety algorithm
In this algorithm, we use vector. Consider vector X and Y. We say X<=YX<=Y if and only if X[i]<=Y[i]X[i] <= Y[i] for all i=1,2,…,ni=1,2,…,n. Each row of Max,Need,AllocationMax,Need,Allocation is a vector.
Safety algorithm check current state: safe or unsafe?

OR pseudo code:
Bool Safe(Current Resource-Allocation State) {
Work <- Available;
for(i: 1 -> n) Finish[i] = false;
flag <- true;
While(flag) {
flag <- false;
for(i: 1 -> n) {
if(Finish[i] = false AND Need[i] <= Work) {
finish[i] = true;
Work <- Work + Allocation[i];
flag = true;
}//endif
}//endwhile
for(i: 1->n) if(finish[i] = false) return false;
return true;
}
}
Resource-Request Algorithm
Data Structure: Request[i]: the request resource vector for thread PiP_{i}. If Request[i][j]=kRequest[i][j] = k then, thread PiP_{i} wants kk instances of resource type RjR_{j}.
Pseudo Code:
Void Resource-Request-Handling(Request[i]) {
if(Request[i] > Need[i])
Error; // has exceeded its maximum claim
if(Request[i] > Available)
Block; // don't enough, wait
// Setup new state
Available = Available - Request[i];
Allocation[i] = Allocation[i] + Request[i];
Need[i] = Need[i] - Request[i];
// check safe or unsafe
if(Safe(New Resource-Allocation State)) {
Allocate(P[i]); // thread P[i] is allocated its resources
}
else {
wait(P[i]); // P[i] wait
// restore old state
Available = Available + Request[i];
Allocation[i] = Allocation[i] - Request[i];
Need[i] = Need[i] + Request[i];
}
}
Practice exercise
Consider the following snapshot of a system:
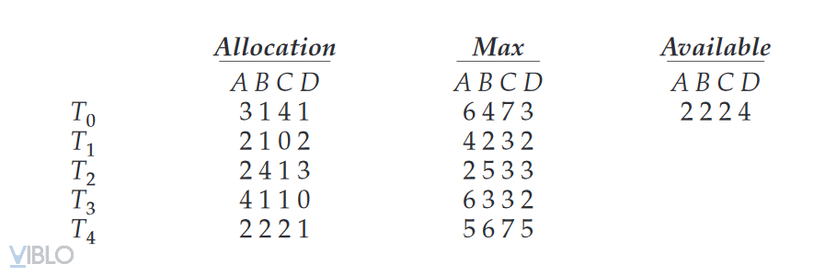
- Illustrate that the system is in a safe state by demonstrating an order in which the threads may complete.
- If a request from thread T4T_{4} arrives for (2,2,2,4)(2, 2, 2, 4), can the request be granted immediately?
Solution:
- The content of NeedNeed matrix is difined to be Max−AllocationMax – Allocation and is as follow:
| Need | A | B | C | D | Allocation | A | B | C | D |
|---|---|---|---|---|---|---|---|---|---|
| T0T_{0} | 3 | 3 | 3 | 2 | T0T_{0} | 3 | 1 | 4 | 1 |
| T1T_{1} | 2 | 1 | 3 | 0 | T1T_{1} | 2 | 1 | 0 | 2 |
| T2T_{2} | 0 | 1 | 2 | 0 | T2T_{2} | 2 | 4 | 1 | 3 |
| T3T_{3} | 2 | 2 | 2 | 2 | T3T_{3} | 4 | 1 | 1 | 0 |
| T4T_{4} | 3 | 4 | 5 | 4 | T4T_{4} | 2 | 2 | 2 | 1 |
This sequence of thread <T2,T3,T4,T0,T1><T_{2}, T_{3},T_{4}, T_{0}, T_{1}> satisfies the safety criteria. This state is safe.
- Request[4]=(2,2,2,4)≤Need[4]ANDRequest[4]=(2,2,2,4)≤Available.Request[4] = (2,2,2,4) leq Need[4] AND Request[4] = (2,2,2,4) leq Available.
New state:
Available=Available−Request[4]=(0,0,0,0)⇒Available = Available-Request[4] = (0,0,0,0) Rightarrowunsafe⇒Request[4]Rightarrow Request[4] can’t be granted immediately.
References.
- Abraham Silberschatz – Operating System Concepts 10th 2018
- Silde Chater 2 – Thread Manage – Operating System, SoICT, HUST
Nguồn: viblo.asia
