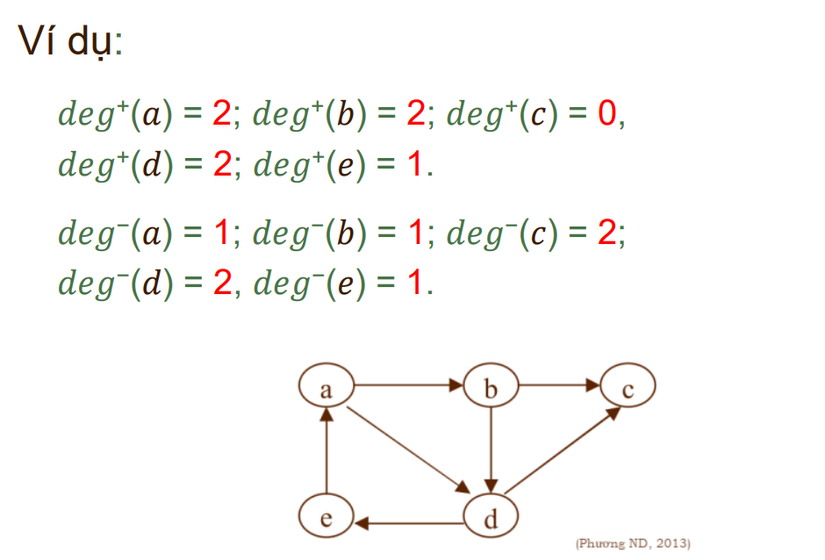
1. Đơn đồ thị vô hướng

Đơn đồ thị vô hướng G = <V,E>, trong đó:
– V (vertext) là tập hợp các đỉnh, các đối tượng, object
– E (Edge) là tập hợp các cặp không có thứ tự gồm 2 phần tử khác của V gọi là các cạnh.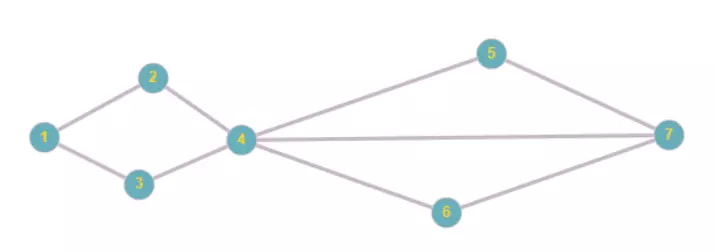

2. Đa đồ thị vô hướng

Đa đồ thị vô hướng G = <V,E>, trong đó:
– V (vertext) là tập hợp các đỉnh, các đối tượng, object
– E là họ các cặp không có thứ tự của 2 đỉnh khác nhau thuộc V gọi là tập các cạnh.
– e1 ∈ E và e2 ∈ E được gọi là cạnh bội nếu chúng tương ứng với một đỉnh.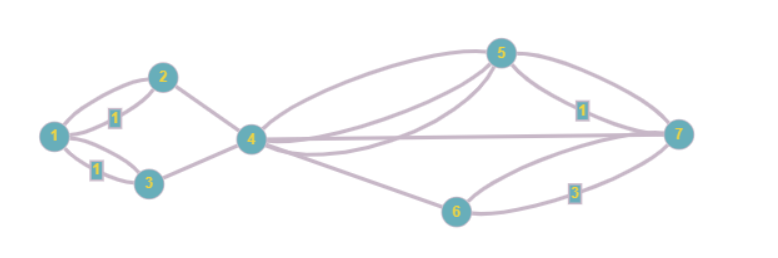

3. Giả đồ thị vô hướng

Giả đồ thị vô hướng G = <V,E>, trong đó:
– E là họ các cặp không có thứ tự gồm 2 phần tử của V không nhất thiết phải khác nhau. Cạnh e được gọi là khuyên nếu e = (u,u)

4. Đơn đồ thị có hướng

Đơn đồ thị có hướng G = <V,E>, trong đó:
– E là tập các cạnh có thứ tự gồm 2 phần tử của V gọi là các cung.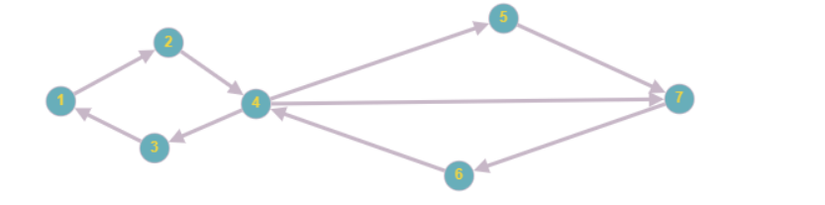

5. Đa đồ thị có hướng

Đa đồ thị có hướng G = <V,E>, trong đó:
– 𝐸 là họ các cặp có thứ tự gồm hai phần tử khác nhau của 𝑉 được gọi là các cung.
– e1∈E && e2∈E cùng tương ứng 1 cặp đỉnh được gọi là cung lặp.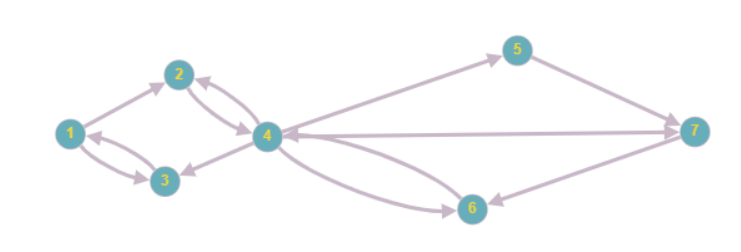

6. Thuật ngữ cơ bản trên đồ thị vô hướng

Định nghĩa 1

Hai đỉnh u,v của đồ thị vô hướng G = <V,E> được gọi là kề nhau khi (u,v) là cạnh thuộc đồ thị G.
Nếu e = (u,v) là cạnh của dồ thị G, thì ta nói cạnh này liên thuộc với 2 đỉnh u,v, đồng thời các đỉnh u và v sẽ được gọi là đỉnh đầu của cạnh (u,v).

Định nghĩa 2

Ta gọi bậc của đỉnh V trong đồ thị vô hướng là số cạnh liên thuộc với nó và kí hiệu là deg(v)deg(1) = deg(3) = deg(4) = 4
deg(5) = 3
deg(2) = 2
deg(6) = 1
deg(7) = 0

Đỉnh bậc 0 gọi là đỉnh cô lập,
Đỉnh bậc 1 gọi là đỉnh treo

7. Định lý về tổng bậc các đỉnh

G = <V,E> là đồ thị vô hướng với m cạnh.
khi đó: Σ deg(v) = 2m.

Với v ∈ V
Chứng minh: với mỗi cạnh e=(u,v), số bậc được tính 1 lần trong deg(u) và được tính 1 lần trong deg(v). Như vậy tổng tất cả các đỉnh sẽ bằng 2 lần số cạnh.

8. Khái niệm về đường đi, chu trình

Đường đi độ dài n từ đỉnh u đến đỉnh v trong đồ thị vô hướng G = <V,E> là dãy xo,x1,x2,…xn. Trong đó n ∈ Z*
xo ∈ u
xn ∈ v
Đường đi có đỉnh đầu trùng đỉnh cuối hay u=v gọi là chu trình
Đường đi hay chu trình được gọi là đơn nếu không có cạnh nào lặp lại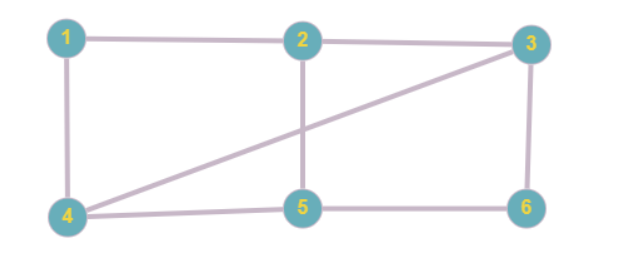

• 1,2,3,4,5,6 là đường đi đơn có độ dài 5.
• 4,5,3,2 không là đường đi vì (5,4) không phải cạnh của đồ thị.
• 1,2,5,4,1,2 có độ dài 5 nhưng không phải đường đi thì (1,2) được lặp 2 lần.

9. Liên thông

Đồ thị vô hướng được gọi là liên thông nếu luôn tìm được đường đi giữa 2 đỉnh bất kì của nó.

10. Bán bậc của đỉnh

Định nghĩa 1:

Nếu e=(u,v) là cung của đồ thị có hướng G=(V,E), ta nói:

• 2 đỉnh u,v là kề nhau
• kí hiệu (u,v): đi ra từ đỉnh u, đi vào đỉnh v
• u là đỉnh đầu, v là đỉnh cuối

Định nghĩa 2:

• Ta gọi bán bậc ra của đỉnh 𝑣 trên đồ thị có hướng là số
  cung của đồ thị đi ra khỏi 𝑣 và ký hiệu là 𝑑𝑒𝑔+
  (𝑣).
• Ta gọi bán bậc vào của đỉnh 𝑣 trên đồ thị có hướng là số cung của đồ thị đi vào 𝑣 và ký hiệu là 𝑑𝑒𝑔− (𝑣)