Chương 3: LINKED LISTS – 8.Problems & Solutions(11-20)

Problem-11

Chúng tôi được cung cấp một con trỏ đến phần tử đầu tiên của một danh sách liên kết L.
Có hai khả năng xảy ra đối với L, nó kết thúc (con rắn) hoặc phần tử cuối cùng của nó trỏ về một trong những phần tử trước đó trong danh sách (con ốc sên).
Đưa ra một thuật toán kiểm tra xem một danh sách cho trước L là một con rắn hay một con ốc sên.

Solution:
Nó cũng giống như Problem-7.

Problem-12

Kiểm tra xem danh sách liên kết đã cho có phải là kết thúc NULL hay không. Nếu có một chu trình, hãy tìm nút bắt đầu của vòng lặp.

Solution:
Giải pháp là một phần mở rộng cho giải pháp trong Problem-10.
Sau khi tìm thấy vòng lặp trong danh sách được liên kết, chúng tôi khởi tạo slowPtr về đầu danh sách liên kết.
Từ thời điểm đó trở đi, cả slowPtr và fastPtr chỉ di chuyển một nút tại một thời điểm.
Điểm mà chúng gặp nhau là điểm bắt đầu của vòng lặp.
Nói chung, chúng ta sử dụng phương pháp này để loại bỏ các vòng lặp.
Gọi x và y là những du khách sao cho y đi nhanh gấp đôi x (tức là y = 2x).
Đặt s là nơi x và y lần đầu tiên gặp nhau và bắt đầu đi bộ cùng một lúc.
Sau đó, khi x và y gặp lại nhau lần tiếp theo, khoảng cách từ s đến điểm bắt đầu của vòng lặp chính xác bằng khoảng cách từ địa điểm gặp nhau hiện tại của x và y đến đầu của vòng lặp.

	private static ListNode findBeginOfLoop(ListNode head) {
		ListNode fastPtr = head;
		ListNode slowPtr = head;
		boolean loopExists = false;
		while(fastPtr != null && fastPtr.getNext() != null) {
			fastPtr = fastPtr.getNext().getNext();
			slowPtr = slowPtr.getNext();
			if(slowPtr == fastPtr) {
				loopExists = true;
				break;
			}
		}
		
		if(loopExists) {
			slowPtr = head;
			while(slowPtr != fastPtr) {
				fastPtr = fastPtr.getNext();
				slowPtr = slowPtr.getNext();
			}
			return fastPtr;
		} else {
			return null;
		}
	}

Problem-13

Chứng minh thuật toán trên là đúng.

Solution:
Vấn đề này là trọng tâm của lý thuyết số.
Trong thuật toán tìm chu trình Floyd, lưu ý rằng rùa và thỏ rừng sẽ gặp nhau khi chúng có kích thước n × L, trong đó L là độ dài vòng lặp.
Hơn nữa, con rùa nằm ở điểm giữa giữa thỏ rừng và đầu chuỗi vì cách chúng di chuyển.
Do đó, con rùa cũng cách đầu dãy n × L.
Nếu chúng ta di chuyển cả hai bước tại một thời điểm, từ vị trí của con rùa và từ đầu chuỗi, chúng ta biết rằng chúng sẽ gặp nhau ngay khi cả hai ở trong vòng lặp, vì chúng là n × L, bội số của độ dài vòng lặp, cách nhau.
Một trong số chúng đã ở trong vòng lặp, vì vậy chúng tôi chỉ di chuyển bước còn lại trong một bước duy nhất cho đến khi nó đi vào vòng lặp, giữ cho n × L khác luôn tránh xa nó.

😅 đoạn giải thích này tác giả viết quả thật hơi mông lung, mình đọc cũng cảm thấy khó hiểu, nên mình có tham khảo ở đây, hoặc nếu muốn xem video cho sinh động thì ở đây

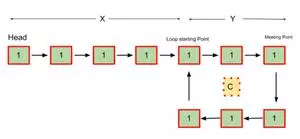
Đặt
X = Khoảng cách giữa đầu (bắt đầu) đến điểm bắt đầu của vòng lặp.
Y = Khoảng cách giữa điểm bắt đầu của vòng lặp và điểm gặp nhau đầu tiên của cả hai con trỏ.
C = Độ dài của vòng lặp

Thời điểm 2 con trỏ gặp nhau lần đầu tiên:

• Con trỏ chậm đã đi được quãng đường $X+Y+s\ast C$, trong đó s là một hằng số dương bất kỳ.
• Con trỏ nhanh đã đi được quãng đường $X+Y+f\ast C$, trong đó f là một hằng số dương bất kỳ.

Vì con trỏ nhanh tốc độ gấp đôi con trỏ chậm nên thời điểm gặp nhau quãng đường con trỏ nhanh đi được sẽ gấp đôi con trỏ chậm
=> $X+Y+f\ast C=2\ast (X+Y+s\ast C)$
$X+Y=f\ast C–2\ast s\ast C$
$f\ast C–2\ast s\ast C=(someinteger)\ast C=K\ast C$

Vậy ta được:
$X+Y=K\ast C$ – ( 1 )
$X=K\ast C–Y$ – ( 2 )
Với K là một hằng số dương bất kỳ

• Bây giờ nếu đặt lại con trỏ chậm về đầu (vị trí bắt đầu) và di chuyển con trỏ nhanh và chậm từng đơn vị một, người ta có thể quan sát từ phương trình thứ nhất và thứ hai mà cả hai sẽ gặp nhau sau khi đi được quãng đường X ở điểm bắt đầu vòng lặp vì sau khi đặt lại con trỏ chậm và di chuyển nó khoảng cách X, đồng thời từ điểm gặp của vòng lặp, con trỏ nhanh cũng sẽ di chuyển quãng đường $K\ast C-Y$ (vì nó đã đi được quãng đường Y).
• Từ phương trình (2), ta có $X=K\ast C-Y$, do đó, cả hai con trỏ sẽ di chuyển quãng đường X tức là cùng một khoảng cách để gặp nhau tại điểm bắt đầu của chu kỳ.

Problem-15

Kiểm tra xem danh sách liên kết đã cho có phải là kết thúc NULL hay không. Nếu có một chu kỳ, hãy tìm độ dài của vòng lặp.

Solution:
Giải pháp này cũng là một phần mở rộng của bài toán phát hiện chu trình cơ bản.
Sau khi tìm thấy vòng lặp trong danh sách được liên kết, hãy giữ nguyên slowPtr.
FastPtr tiếp tục di chuyển cho đến khi nó quay trở lại slowPtr.
Lúc này con trỏ fastPtr di chuyển từng bước một.

	private static int findLengthOfTheLoop(ListNode head) {
		ListNode fastPtr = head;
		ListNode slowPtr = head;
		boolean loopExists = false;
		while(fastPtr != null && fastPtr.getNext() != null) {
			fastPtr = fastPtr.getNext().getNext();
			slowPtr = slowPtr.getNext();
			if(slowPtr == fastPtr) {
				loopExists = true;
				break;
			}
		}
		int length = 0;
		if(loopExists) {
			do {
				slowPtr = slowPtr.getNext();
				length++;
			} while(slowPtr != fastPtr);
		} 
		return length;
	}

Time Complexity: O(n).
Space Complexity: O(1).

Problem-16

Chèn một nút vào danh sách liên kết được sắp xếp

Solution:
Duyệt qua list và tìm vị trí phù hợp và insert.

	public ListNode InsertInSortedList(ListNode head, ListNode newNode) {
		ListNode current = head;
		ListNode temp = head;
		if(head == null) {
			return newNode;
		}
		
		//traverse the list until you find item bigger the new node value
		while(current != null && current.getData() < newNode.getData()) {
			 temp = current;
			 current = current.getNext();
		}
		
		//insert the new node before the big item
		newNode.setNext(current);
		temp.setNext(newNode);
		return head;
	}

Time Complexity: O(n).
Space Complexity: O(1).

Problem-17

Đảo ngược một danh sách được liên kết đơn.

Solution:
Iterative version:

	public ListNode reverseListIterative(ListNode head) {
		ListNode current = head;
		ListNode prev = null;
		
		while(current != null) {
			ListNode next = current.getNext();
			current.setNext(prev);
			prev = current;
			current = next;
		}
		
		return prev;
	}

Time Complexity: O(n).
Space Complexity: O(1).

Recursive version:

	public void reverseListRecursive(ListNode current, ListNode[] head) {
		if(current == null) {
			return;
		}
		
		ListNode next = current.getNext();
		if(next == null) {
			head[0] = current;
			return;
		}
		
		reverseListRecursive(next, head);
		
		//Make next node points to current node
		next.setNext(current);
		
		//Remove existing link
		current.setNext(null);
	}

Time Complexity: O(n).
Space Complexity: O(n), sử dụng cho stack đệ quy

Problem-18

Giả sử có hai danh sách được liên kết đơn lẻ, cả hai đều cắt nhau tại một số điểm và trở thành một danh sách được liên kết duy nhất.
Con trỏ đầu hoặc con trỏ bắt đầu của cả hai danh sách đều được biết đến, nhưng nút giao nhau không được biết.
Ngoài ra, số lượng các nút trong mỗi danh sách trước khi chúng giao nhau là không xác định và có thể khác nhau trong mỗi danh sách.
List1 có thể có n nút trước khi nó đến giao điểm và List2 có thể có m nút trước khi nó đến giao điểm trong đó m và n có thể là $m=n,m<n$ hoặc $m>n$.
Đưa ra giải thuật tìm điểm hợp nhất.

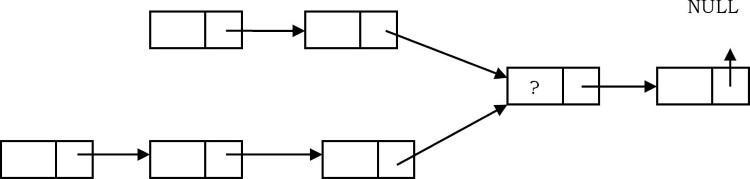
Solution: Brute-Force Approach
Một giải pháp đơn giản là so sánh mọi con trỏ nút trong danh sách đầu tiên với mọi con trỏ nút khác trong danh sách thứ hai mà theo đó các con trỏ nút phù hợp sẽ dẫn chúng ta đến nút giao nhau.
Tuy nhiên, độ phức tạp về thời gian trong trường hợp này sẽ là $O(mn)$ sẽ cao.

Time Complexity: $O(mn)$.
Space Complexity: $O(1)$

Problem-19

Chúng ta có thể giải quyết Problem-18 bằng cách sử dụng kỹ thuật sắp xếp không?

Solution:No.Hãy xem xét thuật toán sau dựa trên việc sắp xếp và xem tại sao thuật toán này không thành công.
Algorithm:

• Lấy các con trỏ nút danh sách đầu tiên và giữ chúng trong một số mảng và sắp xếp chúng.
• Lấy các con trỏ nút danh sách thứ hai và giữ chúng trong một số mảng và sắp xếp chúng.
• Sau khi sắp xếp, hãy sử dụng hai index: một cho mảng được sắp xếp đầu tiên và một cho mảng được sắp xếp thứ hai.
• Bắt đầu so sánh các giá trị tại các index và tăng index theo giá trị nào có giá trị thấp hơn (chỉ tăng nếu các giá trị không bằng nhau).
• Tại bất kỳ thời điểm nào, nếu chúng ta có thể tìm thấy hai index có giá trị giống nhau, thì điều đó chỉ ra rằng hai nút đó đang trỏ đến cùng một nút và chúng ta trả về nút đó.

Time Complexity: Thời gian sắp xếp danh sách + Thời gian quét (để so sánh) $=O(mlogm)+O(nlogn)+O(m+n)$
Chúng ta cần xem xét một trong những cung cấp cho giá trị lớn nhất.
Space Complexity: $O(1)$.

Thuật toán trên có vấn đề gì không? Yes. Trong thuật toán, chúng ta đang lưu trữ tất cả danh sách và sắp xếp chúng. Nhưng chúng ta đang quên một thực tế là có thể có nhiều phần tử lặp lại. Điều này là do sau điểm hợp nhất, tất cả các con trỏ nút đều giống nhau cho cả hai danh sách. Thuật toán chỉ hoạt động tốt trong một trường hợp và đó là khi cả hai danh sách đều có nút kết thúc tại điểm hợp nhất của chúng.

Problem-20

Chúng ta có thể giải quyết Problem-18 bằng cách sử dụng hash tables?

Solution: Yes.
Algorithm:

• Chọn một danh sách có số nút ít hơn (Nếu chúng ta không biết trước độ dài thì hãy chọn ngẫu nhiên một danh sách).
• Bây giờ, duyệt qua danh sách khác và đối với mỗi con trỏ nút của danh sách này, hãy kiểm tra xem con trỏ nút giống nhau có tồn tại trong bảng băm hay không.
• Nếu có một điểm hợp nhất cho các danh sách đã cho thì chắc chắn chúng ta sẽ gặp trong bảng băm.

Time Complexity: Thời gian tạo bảng băm + Thời gian quét danh sách thứ hai = $O(m)+O(n)$ (hoặc $O(n)+O(m)$, tùy thuộc vào danh sách mà chúng ta chọn để tạo bảng băm.
Space Complexity: $O(n)$ or $O(m)$.