Chương 1: Introduction – 10.Algorithms Analysis: Problems & Solutions(31-40)

Problem-31

Xác định giới hạn Θ cho hàm sau: $T(n)=T(\lceil n/2\rceil )+7$
Solution: Sử dụng Master Theorem
ta được: $\Theta (logn)$

Problem-32

Chứng minh rằng running time của đoạn code sau là $\Omega (logn)$

	public void Read(int n) {
		int k = 1;
		while(k < n) {
			k = 3*k;
		}
	}

Solution: Vòng lặp while sẽ kết thúc khi giá trị của ‘k’ lớn hơn hoặc bằng giá trị của ‘n’.
Trong mỗi lần lặp, giá trị của ‘k’ được nhân với 3.
Nếu i là số lần lặp, thì ‘k’ có giá trị là 3*i sau i lần lặp.
Vòng lặp được kết thúc khi đạt đến lần lặp thứ i khi 3i≥n3 ^ { i } geq n3i≥n↔i≥log⁡3nleftrightarrow i geq log _ { 3 } n↔i≥log3​n
Điều này cho thấy $i=\Omega (logn)$.

Problem-33

Tìm độ phức tạp:

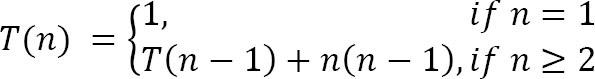
Solution: Bằng cách lặp lại ta có:

$T(n)=T(n-2)+(n-1)(n-2)+n(n-1)$
…
T(n)=T(1)+∑i=1ni(i−1)T ( n ) = T ( 1 ) + sum _ { i = 1 } ^ { n } i ( i – 1 )T(n)=T(1)+∑i=1n​i(i−1)

T(n)=T(1)+∑i=1ni2−∑i=1niT ( n ) = T ( 1 ) + sum _ { i = 1 } ^ { n } i ^ { 2 } – sum _ { i = 1 } ^ { n } iT(n)=T(1)+∑i=1n​i2−∑i=1n​i

T(n)=1+n(n+1)(2n+1)6−n(n+1)2T ( n ) = 1 + frac { n ( n + 1 ) ( 2 n + 1 ) } { 6 } – frac { n ( n + 1 ) } { 2 }T(n)=1+6n(n+1)(2n+1)​−2n(n+1)​

T(n)=Θ(n3)T ( n ) = Theta ( n ^ { 3 } )T(n)=Θ(n3)

Chứng minh tổng của bình phương i -> n:

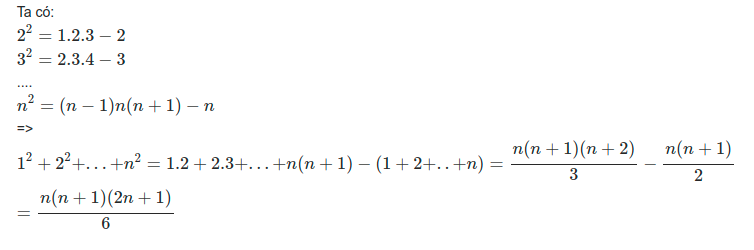
Note: Chúng ta cũng có thể sử dụng Subtraction and Conquer master theorem để tìm ra đáp án.

Problem-34

Solution: Bài toán Fibonacci

Problem-35

Tìm độ phức tạp:

	public void Funtion(int n) {
		for(int i = 1; i <= n; i++) {
			for(int j = 1; j <= n; j += i)
				System.out.println("*");
		}
	}

Solution: Xem xét đoạn code cùng với comment:

	public void Funtion(int n) {
        // Vòng lặp này thực thi n lần
		for(int i = 1; i <= n; i++) {
            \Vòng lặp này thực hiện j lần với j tăng theo tốc độ của i
			for(int j = 1; j <= n; j += i)
				System.out.println("*");
		}
	}

Trong chương trình trên, vòng lặp bên trong thực hiện n / i lần cho mỗi giá trị của i => Running time: (∑i=1nn/i)−=O(nlogn)( sum _ { i = 1 } ^ { n } n / i ) ^ { – } = O ( n l o g n )(∑i=1n​n/i)−=O(nlogn)
Harmonic series

Problem-36

Tìm độ phức tạp: ∑i=1nlogisum _ { i = 1 } ^ { n } l o g i∑i=1n​logi
Solution: Sử dụng thuộc tính logarit $logxy=logx+logy$, tổng trên tương đương với
∑i=1nlogi=log1+log2+…+logn=log(1∗2∗3∗…∗n)=log(n!)≤log(nn)≤nlog(n)sum _ { i=1 } ^ { n } log i = log1 +log2 + … + logn = log(1*2*3*…*n) = log(n!) leq log(n^n) leq nlog(n)∑i=1n​logi=log1+log2+…+logn=log(1∗2∗3∗…∗n)=log(n!)≤log(nn)≤nlog(n)
=> Time Complexity: $O(nlogn)$

Problem-37

Tìm độ phức tạp:

	public void Funtion(int n) {
        if(n <= 1) return;
		for(int i = 1; i <= 3; i++) {
			Funtion(n/3);
		}
	}

Solution: Xem xét comment:

	public void Funtion(int n) {
        //constant time
        if(n <= 1) return;
        //Vòng lặp này thực hiện với vòng lặp đệ quy có giá trị n/3
		for(int i = 1; i <= 3; i++) {
			Funtion(n/3);
		}
	}

Function đã cho có dạng: T(n)=3T(n3)+Θ(1)T ( n ) = 3 T ( frac { n } { 3} ) + Theta ( 1 )T(n)=3T(3n​)+Θ(1). Sử dụng master theorem , ta được $T(n)=\Theta (n)$.

Problem-38

Tìm độ phức tạp:

	public void Funtion(int n) {
        if(n <= 1) return;
		for(int i = 1; i <= 3; i++) {
			Funtion(n-1);
		}
	}

Solution: Xem xét comment:

	public void Funtion(int n) {
        //constant time
        if(n <= 1) return;
        //Vòng lặp này thực hiện với vòng lặp đệ quy có giá trị n-1
		for(int i = 1; i <= 3; i++) {
			Funtion(n-1);
		}
	}

Câu lệnh if yêu cầu constant time O(1).
Với vòng lặp for, chúng ta bỏ qua chi phí vòng lặp và chỉ đếm ba lần hàm được gọi đệ quy. Ta có công thức sau:

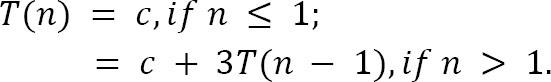
Sử dụng Subtraction and Conquer master theorem ta được T(n)=Θ(3n)T ( n ) = Theta ( 3 ^ { n } )T(n)=Θ(3n)

Problem-39

Tìm độ phức tạp:

	public void Funtion(int n) {
        if(n <= 1) return;
		for(int i = 1; i <= n; i++) {
            System.out.println("*");
		}
			Funtion(0.8*n);
	}

Solution: Xem xét comment:

	public void Funtion(int n) {
        //constant time
        if(n <= 1) return;
        //Vòng lặp này thực thi n lần
		for(int i = 1; i <= n; i++) {
            System.out.println("*");
		}
		Funtion(0.8*n);
	}

Ta được công thức như sau: T(n)=T(0.8n)+O(n)=T(45n)+O(n)=45T(n)+O(n)T ( n ) = T ( text 0.8 n ) { + } O ( n ) = T ( frac { 4 } { 5 n } ) + O ( n ) = frac { 4 } { 5 } T ( n ) + O ( n )T(n)=T(0.8n)+O(n)=T(5n4​)+O(n)=54​T(n)+O(n)
Sử dụng master theorem , ta được $T(n)=O(n)$

Problem-40

Tìm độ phức tạp: T(n)=2T(n)+lognT ( n ) = 2 T ( sqrt { n } ) + l o g nT(n)=2T(n​)+logn
Solution: Hàm đệ quy đã cho không ở định dạng master theorem nào. Chúng ta hãy thử chuyển nó sang dạng định lý chính bằng cách giả sử n=2mn = 2^mn=2m.
Áp dụng lôgarit cả hai vế ta được: $logn=mlog2\Rightarrow m=logn$
Bây giờ, hàm đã cho trở thành:
T(n)=T(2m)=2T(2m)+m=2T(2m2)+mT ( n ) = T ( 2 ^ { m } ) = 2 T ( sqrt { 2 ^ { m } } ) + m = 2 T ( 2 ^ { frac { m } { 2 } } ) + mT(n)=T(2m)=2T(2m​)+m=2T(22m​)+m

Để làm cho nó đơn giản, chúng ta giả định
S(m)=T(2m)⇒S(m2)=T(2m2)S ( m ) = T ( 2 ^ { m } ) Rightarrow S ( frac { m } { 2 } ) = T ( 2 ^ { frac { m } { 2 } } )S(m)=T(2m)⇒S(2m​)=T(22m​)
Thay vào công thức trên ta được: S(m)=2S(m2)+mS ( m ) = 2 S ( frac { m } { 2 } ) + mS(m)=2S(2m​)+m
Sử dụng master theorem ta có kết quả:
$S(m)=O(mlogm)$
Thay $m=logn$ trở lại ta được: $T(n)=S(logn)=O(log(n)loglogn)$