Bài viết này mình sẽ trình bày chi tiết về cách mà chúng ta sẽ biểu diễn 3 trường hợp xảy ra với 1 hàm toán học như đã trình bày ở trên sử dụng các kí hiệu và đồ thị để minh họa.
1.11 Asymptotic Notation – Ký hiệu tiệm cận
Chúng ta đã biết các biểu thức cho các trường hợp tốt nhất, trung bình và xấu nhất, đối với cả ba trường hợp, chúng ta cần xác định giới hạn trên và giới hạn dưới.
Để thể hiện các giới hạn trên và dưới này, chúng ta cần một số loại cú pháp, và đó là chủ đề mà chúng ta sẽ thảo luận tiếp theo.
Giả sử rằng thuật toán đã cho được biểu diễn dưới dạng hàm f (n).
1.12 Big-O Notation
Ký hiệu này cung cấp upper bound(giới hạn/tiệm cận trên) của hàm đã cho.
Nó được biểu diễn dưới dạng f(n) = O(g(n)).
Điều này có nghĩa là, với các số n có giá trị lớn, tiệm cận trên của f(n) là g(n).
Đồ thị cho mọi người dễ hình dung:
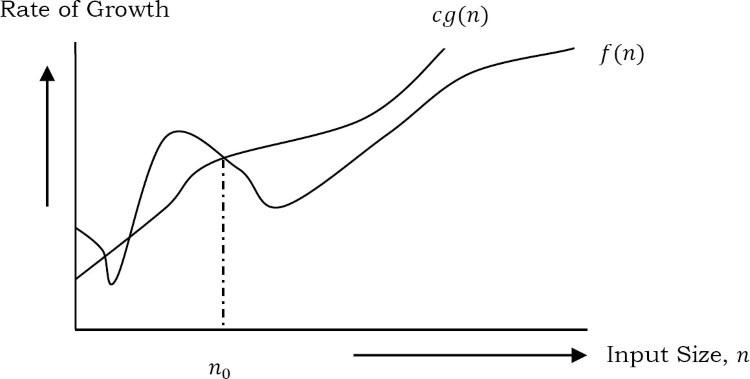
Như ví dụ ở bài viết trước, nếu f (n) = n^4 + (2 * n^2) + 100n + 500 là hàm số biểu diễn cho thuật toán đã cho, thì n^4 là g(n).
Nguyên văn tiếng anh: “That means g(n) gives the maximum rate of growth for f(n) at larger values of n.”
Hiểu một cách đơn giản, g(n) là một hàm số mà tốc độ biến thiên của nó tương ứng với hàm số f(n) khi n tăng lên rất lớn.
OK, chúng ta sẽ xem xét kí hiệu O-notation chi tiết hơn 1 chút.
O–notation được định nghĩa như sau:
O(g(n)) = {f(n): tồn tại các hằng số dương c và n0 sao cho 0 ≤ f(n) ≤ c * g(n) với mọi n ≥ n0}.*
=> g(n) là một asymptotic tight upper bound(hiểu đơn giản là tiệm cận trên) đối với hàm f(n).
Nhìn chung, chúng ta sẽ loại bỏ các giá trị thấp của n. Điều này có nghĩa là rate of growth ở các giá trị thấp của n là không quan trọng.
Trong hình, n0 là điểm mà từ đó chúng ta cần xem xét rate of growth của một thuật toán nhất định.
Dưới n0, rate of growth có thể khác.
=>n0 được gọi là ngưỡng của hàm đã cho.
Chỗ này hơi trừu tượng một chút nên mình sẽ giải thích thêm: như ví dụ trước mình đã lấy ở thuật toán sắp xếp, thì nếu như mảng đầu vào chỉ có 1 số lượng rất ít phần tử(giả sử là 10 hay 20), thì khối lượng tính toán sẽ rất ít và thời gian xử lý là vô cùng nhanh, gần như không đáng kể nên có thể bỏ qua.
Mọi thứ chỉ bắt đầu khó khăn và phức tạp khi độ lớn của mảng vượt qua 1 con số nào đó(chính là n0 – ngưỡng của hàm số) => Đây là lí do chúng ta sẽ hầu như chỉ cần quan tâm khi n ≥ n0
Big-O Visualization – Hình dung về Big-O
Nguyên văn tiếng anh: O(g(n)) is the set of functions with smaller or the same order of growth as g(n). ~ một tập hợp các hàm mà có bậc tăng trưởng nhỏ hơn hoặc bằng với g(n)
Ví dụ: O(n^2) bao gồm O(1), O(n), O(nlogn), …
Lưu ý: Chỉ phân tích thuật toán ở các giá trị lớn hơn của n. Điều này có nghĩa là, dưới n0, chúng ta không quan tâm đến rate of growth.
Big-O Examples
Example-1: Tìm upper bound của hàm f(n) = 3n+8
Solution:
Ta đã có định nghĩa: O(g(n)) = {f(n): tồn tại các hằng số dương c và n0 sao cho 0 ≤ f(n) ≤ c * g(n) với mọi n ≥ n0}.*
=> Để tìm upper bound đồng nghĩa với ta phải tìm được hằng số dương c và n0 thỏa mãn điều kiện 0 ≤ f(n) ≤ c * g(n) với mọi n ≥ n0
Với bài toán đã cho: 3n+8 <= 4n với mọi n >= 8
=> Ta có upper bound O(n) với c = 4 và n0 = 8.
Example-2: Tìm upper bound của hàm f(n) = n^2 + 1
Solution: Tương tự example 1, ta đi tìm c và n0
Ta có n^2 + 1 <= 2 * n^2 với mọi n >= 1
=> upper bound O(n^2) với c = 2 và n0 = 1
Example-3: Tìm upper bound của hàm f(n) = n^4 + 100 * n^2 + 50
Solution: Ta có n^4 + 100 * n^2 + 50 <= 2 * n^4 với mọi n >= 11
=> upper bound O(n^4) với c = 2 và n0 = 11
(Các bất đẳng thức này chỉ đơn giản là chuyển vế cộng trừ bất đẳng thức rồi khai căn khá đơn giản nên mình sẽ không trình bày lại chi tiết)
Example-4: Tìm upper bound của hàm f(n) = 2n^3 – 2n^2
Solution:
Ta có 2n^3 – 2n^2 <= 2n^3 với mọi n >= 1
=> upper bound O(n^3) với c = 2 và n0 = 1
Example-5: Tìm upper bound của hàm f(n) = n
Solution:
Ta có n <= n với mọi n >= 1
=> upper bound O(n) với c = 1 và n0 = 1
Example-6: Tìm upper bound của hàm f(n) = 410
Solution:
Ta có 410 <= 410 với mọi n >= 1
=> upper bound O(1) với c = 1 và n0 = 1
No Uniqueness?
Không có tập giá trị duy nhất nào cho n0 và c trong việc chứng minh các giới hạn tiệm cận.
Ta hãy xem xét 100n + 5 = O(n). Đối với hàm này, có rất nhiều c và n0 thỏa mãn.
Solution1: 100n + 5 ≤ 100n + n = 101n ≤ 101n, với mọi n ≥ 5, n0 = 5 và c = 101 thỏa mãn.
Solution2: 100n + 5 ≤ 100n + 5n = 105n ≤ 105n, với mọi n ≥ 1, n0 = 1 và c = 105 cũng thỏa mãn.
1.13 Omega-Ω Notation
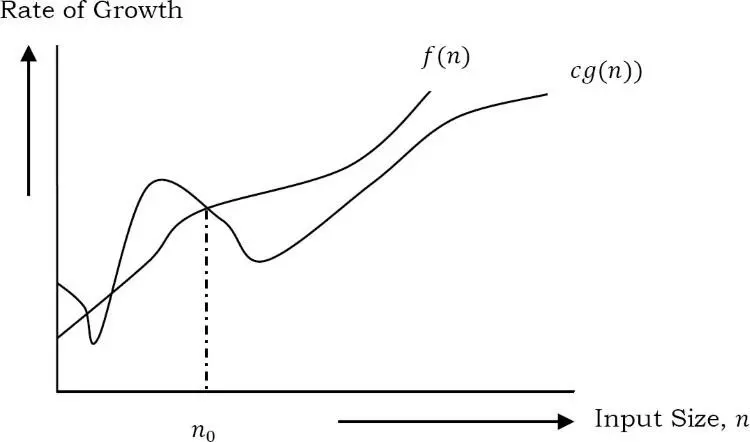
Ký hiệu Ω(đọc là Omega) thể hiện cho tighter lower bound(tiệm cận dưới) của một thuật toán và chúng ta biểu diễn nó dưới dạng f(n) = Ω(g(n))
Điều này có nghĩa với các số n có giá trị lớn, cận dưới của f(n) là g(n). Ví dụ, f(n) = 100 * n^2 + 10n + 50, lower bound là Ω(n^2).
Kí hiệu Ω có thể được định nghĩa là Ω(g(n)) = {f(n): tồn tại các hằng số dương c và n0 sao cho 0 ≤ cg(n) ≤ f(n) với mọi n ≥ n0 }
g(n) là một tiệm cận dưới đối với f(n)
Mục tiêu của chúng ta ở đây là có hàm g(n) có rate of growth lớn nhất nhưng vẫn nhỏ hơn hoặc bằng rate of growth của hàm f(n).
Ω Examples
Example-1: Tìm lower bound của hàm f(n) = 5 * n^2 .
Solution: Tương tự với ví dụ của phần Big O, ở đây ta cũng sẽ đi tìm c và n0 thỏa mãn 0 ≤ cg(n) ≤ f(n) với mọi n ≥ n0
Ta có 0 ≤ c * n^2 ≤ 5n^2 ⇒ c * n^2≤ 5n^2 ⇒ c = 5 and n0 = 1
Example-2: Chứng minh f(n) = 100n + 5 ≠ Ω(n^2 ).
Solution: ∃ c, n0 sao cho: 0 ≤ c * n^2 ≤ 100n + 5
Ta có: 100n + 5 ≤ 100n + 5n (∀n ≥ 1) = 105n
c * n^2 ≤ 105n ⇒ n(c*n – 105) ≤ 0
Vì n là số dương ⇒ cn – 105 ≤ 0 ⇒ n ≤ 105/c
⇒ Mâu thuẫn: n không thể nhỏ hơn một hằng số.(Vì bản chất hàm số f(n) ban đầu không hề có giới hạn nào về giá trị của n)
1.14 Theta-Θ Notation
Ký hiệu này quyết định xem upper và lower bounds của một hàm (thuật toán) đã cho có giống nhau hay không.
Thời gian chạy trung bình của một thuật toán luôn nằm giữa giới hạn dưới và giới hạn trên.
Nếu giới hạn trên (O) và giới hạn dưới (Ω) cho cùng một kết quả, thì ký hiệu Θ cũng sẽ có cùng rate of growth.
Đối với một hàm (thuật toán) nhất định, nếu rate of growth (bounds) đối với O và Ω không giống nhau, thì rate of growth đối với trường hợp Θ có thể sẽ khác.
Trong trường hợp này, chúng ta cần xem xét tất cả các độ phức tạp về thời gian có thể xảy ra và lấy giá trị trung bình của chúng (ví dụ: đối với trường hợp trung bình Quick Sort, khi tới chương về Sắp xếp mình sẽ nói kĩ hơn phần này).
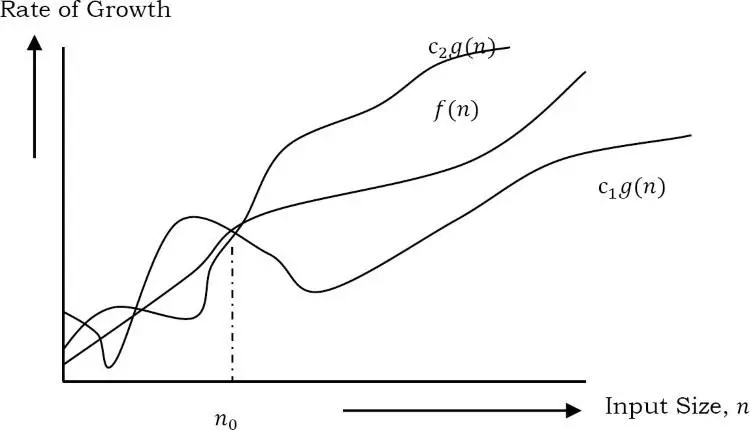
Giờ chúng ta sẽ xem xét kĩ hơn về ký hiệu Θ.
Nó được định nghĩa là Θ(g(n)) = {f(n): tồn tại c1 , c2 and n0 such that 0 ≤ c1 * g(n) ≤ f(n) ≤ c2 * g(n) với mọi n ≥ n0 }.
Θ(g(n)) là tập các hàm có cùng bậc tăng trưởng với g(n).
Θ Examples
Example 1: Tìm Θ bound cho hàm f(n) = (n^2)/2 – n/2
Solution: (n^2)/5 <= (n^2)/2 – n/2 <= n^2 với mọi n >= 2
⇒ Ta có Θ(n^2) với c1 = 1/5, c2 = 1 và n0 = 2.
Example 2: Chứng minh n ≠ Θ(n^2)
Solution: c1 * n^2 <= n <= c2 * n^2
<=> n <= 1/c1 (Vô lý vì không có giới hạn nào về độ lớn của n phải nhỏ hơn 1 số nào đó).
Example 3: Chứng minh 6 * n^3 ≠ Θ(n^2)
Solution: c1 * n^2 ≤ 6 * n^3 ≤ c2 * n^2
⇒ n ≤ c2/6 (Vô lý vì không có giới hạn nào về độ lớn của n phải nhỏ hơn 1 số nào đó).
Example 4: Chứng minh n ≠ Θ(logn)
Solution: c1 * log(n) <= n <= c2 * log(n)
⇒ Ta có vế phải c2 >= n/log(n) với mọi n >= n0 (Vô lý vì không thể tồn tại 1 số dương c2 mà n/log(n) luôn nhỏ hơn với mọi n > n0).
Tạm kết – Với 1 lưu ý quan trọng
Để phân tích (best case, worst case and average), chúng ta đã có upper bound (O), lower bound (Ω) và average running time (Θ).
Từ các ví dụ trên, cũng cần thấy rõ rằng, đối với một hàm (thuật toán) nhất định, việc lấy upper bound (O), lower bound (Ω) và average running time (Θ) có thể không phải lúc nào cũng khả thi.
Trong các chương còn lại, chúng ta sẽ tập trung vào upper bound (O) vì biết lower bound (Ω) của một thuật toán không có tầm quan trọng trong thực tế và chúng ta sẽ sử dụng ký hiệu Θ nếu upper bound (O) và lower bound (Ω) là giống nhau.
Nguồn: viblo.asia
