Chương 6: TREES – 6.Cây biểu thức(Expression Trees)

Nhân ngày mùng một Tết khai bút đầu xuân, mình xin được chúc tất cả mọi người một năm mới thật nhiều sức khỏe, thành công và nhiều may mắn trong cuộc sống. Hi vọng trong năm nay mình sẽ hoàn thành được series này.

6.7 Expression Trees

Cây biểu diễn một biểu thức được gọi là cây biểu thức(Expression Trees).
Trong cây biểu thức, các nút lá là toán hạng và các nút không phải lá là toán tử.
Điều đó có nghĩa là, một cây biểu thức là một cây nhị phân trong đó các nút bên trong là toán tử và các lá là toán hạng.
Một cây biểu thức bao gồm biểu thức nhị phân.
Nhưng đối với toán tử một ngôi, một cây con sẽ trống.
Hình dưới đây cho thấy một cây biểu thức đơn giản cho $(A+B\ast C)/D$.

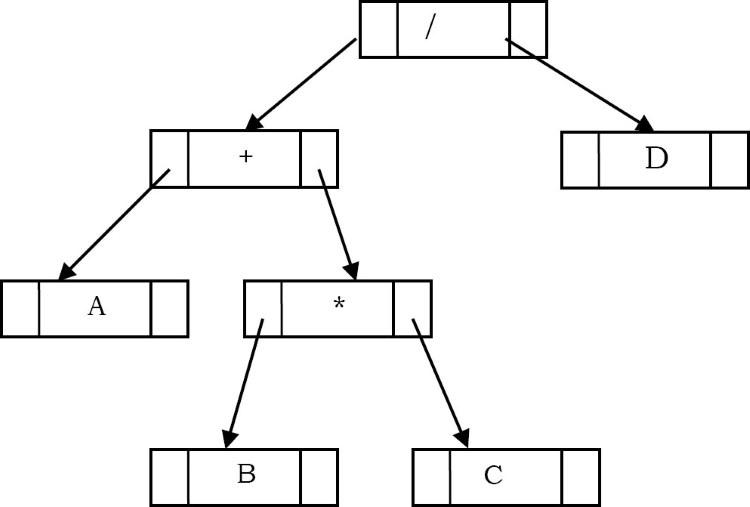
Trong một biểu thức hậu tố(Postfix Expression), một toán tử được viết sau các toán hạng của nó. Mọi người có thể tham khảo thêm định nghĩa và cách chuyển đổi các loại biểu thức này ở đây và ở đây

Thuật toán xây dựng Expression Trees từ Postfix Expression

Bây giờ để xây dựng cây biểu thức, chúng ta sử dụng ngăn xếp. Chúng ta lặp qua biểu thức đầu vào và thực hiện các thao tác sau cho mọi ký tự.

1. Nếu một ký tự là một toán hạng, hãy push ký tự đó vào ngăn xếp
2. Nếu một ký tự là toán tử, hãy pop hai giá trị từ ngăn xếp, biến chúng thành con của nó và đẩy lại nút hiện tại.
   Cuối cùng, phần tử duy nhất của ngăn xếp sẽ là gốc của cây biểu thức.

Code của thuật toán này mình có tham khảo ở đây

import java.util.Stack;
 
class Node{
    char data;
    Node left,right;
    public Node(char data){
        this.data = data;
        left = right = null;
    }
}
 
public class Main {
    public static boolean isOperator(char ch){
        if(ch=='+' || ch=='-'|| ch=='*' || ch=='/' || ch=='^'){
            return true;
        }
        return false;
    }
    public static Node expressionTree(String postfix){
        Stack<Node> st = new Stack<Node>();
        Node t1,t2,temp;
 
        for(int i=0;i<postfix.length();i++){
            if(!isOperator(postfix.charAt(i))){
                temp = new Node(postfix.charAt(i));
                st.push(temp);
            }
            else{
                temp = new Node(postfix.charAt(i));
 
                t1 = st.pop();
                t2 = st.pop();
 
                temp.left = t2;
                temp.right = t1;
 
                st.push(temp);
            }
 
        }
        temp = st.pop();
        return temp;
    }
    public static void inorder(Node root){
        if(root==null) return;
 
        inorder(root.left);
        System.out.print(root.data);
        inorder(root.right);
    }
    public static void main(String[] args) {
        String postfix = "ABC*+D/";
 
        Node r = expressionTree(postfix);
        inorder(r);
    }
}

Mô tả cụ thể cách thuật toán hoạt động

Giả sử rằng một phần tử được đọc tại một thời điểm.
Nếu phần tử là một toán hạng, chúng ta tạo một node và push nó vào một ngăn xếp.
Nếu phần tử là một toán tử, pop hai cây T1 và T2 từ ngăn xếp (T1 được pop lên trước) và tạo thành một cây mới có gốc là toán tử và các con bên trái và bên phải của nó lần lượt trỏ tới T2 và T1.
Node mới này sau đó được đẩy vào ngăn xếp.
Ví dụ: giả sử đầu vào là ABC*+D/.
Ba biểu tượng đầu tiên là toán hạng, vì vậy hãy tạo các nút cây và đẩy các con trỏ tới chúng vào một ngăn xếp như hình bên dưới.

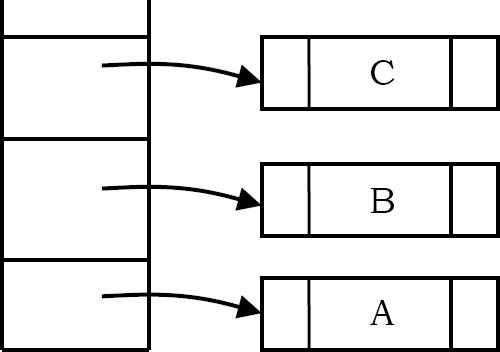
Tiếp theo, một toán tử ‘*’ được đọc, do đó, hai node được bật ra, một cây mới được hình thành và một node mới được đẩy vào ngăn xếp.

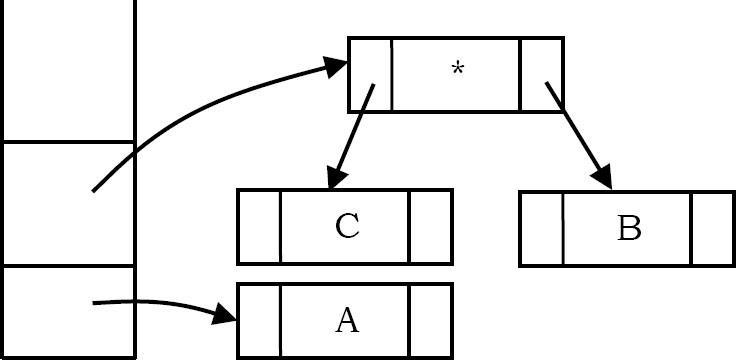
Tiếp theo, toán tử ‘+’ được đọc, do đó, hai node được bật ra, một cây mới được hình thành và một node mới được đẩy vào ngăn xếp.

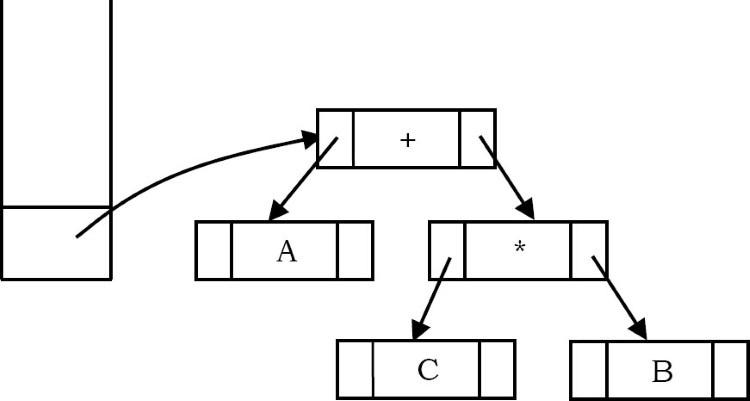
Tiếp theo, toán hạng ‘D’ được đọc, cây một nút được tạo và con trỏ tới cây tương ứng được đẩy vào ngăn xếp.

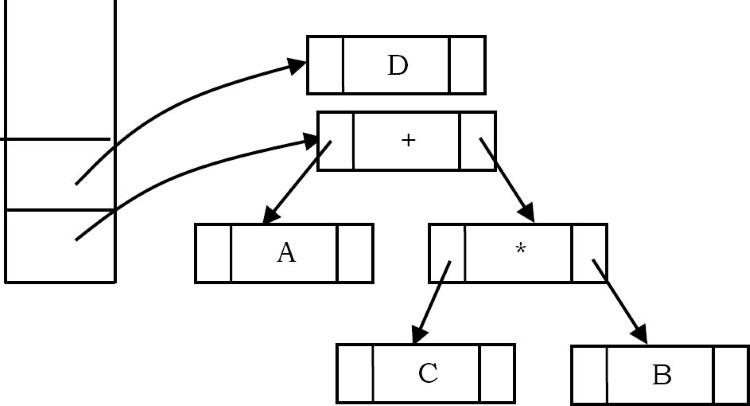
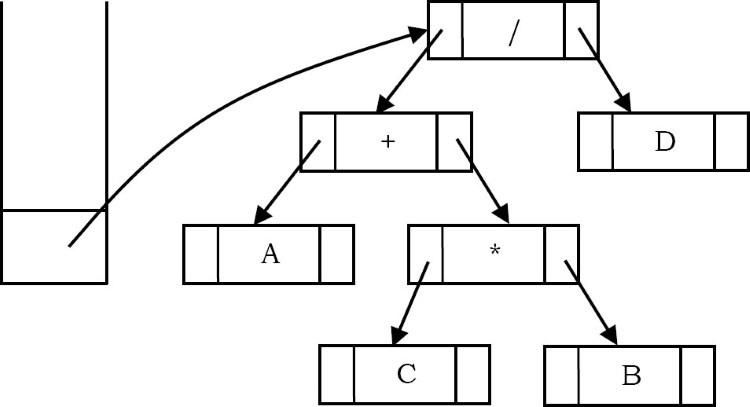
Cuối cùng, ký hiệu cuối cùng (‘/’) được đọc, hai cây được hợp nhất và một con trỏ tới cây cuối cùng được để lại trên ngăn xếp.